Why are Contour Integrals defined the way they are?

Question

I have a question about Contour Integrals.

Contour Integrals are defined as $$\int_{C} f(z)dz = \int_{a}^{b} f(z(t))z'(t)dt \tag{1}$$.
But why define it this way?

The textbook I'm using (Complex Variables and Applications by Brown and Churchill) simply gave this definition with little explanation. I read that Contour Integrals have no geometric interpretation and are used instead to help evaluate real-valued definite integrals. But as someone who just finished Calculus 2 and 3 where all the integrals were constructed from Riemann Sums and had a clear geometric meaning, this seems strange to me.

I notice that this definition looks similar to the definition of a line integral from Calculus 3, $$\int_{a}^{b} f(r(t))|r'(t)|dt \tag{2}$$.
But they are not quite the same.

Can anyone please explain that?

Answer 1

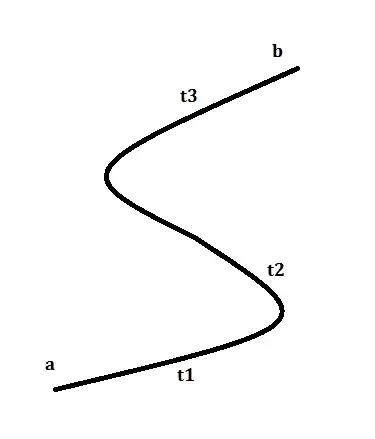
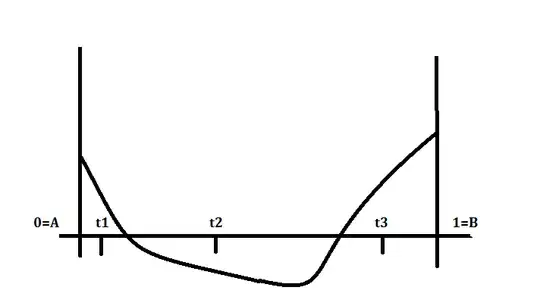
A more natural way to define them is analogous to Riemann sums. Indeed for the usual Riemann integral we would define

$$\int_a^bf(x)\,\mathrm{d}x:=\lim_{\lVert\mathcal{P}\rVert\to0}\sum_{j=1}^nf(x_j^*)(x_j-x_{j-1}),$$

where the limit is taken over all tagged partitions $\mathcal{P}$ of $[a,b]$. Say we instead want to integrate along a curve $\gamma$. Then a very natural way to do this would be to replace the $x_j-x_{j-1}$ with $\gamma(x_j)-\gamma(x_{j-1})$, i.e. the distance between two points on the curve, and to replace $x_j^*$ with $\gamma(x_j^*)$, as we wish to evaluate our function at a point on the curve between the two we just measured the distance of. This leads us to defining

$$\int_\gamma f(z)\,\mathrm{d}z:=\lim_{\lVert\mathcal{P}\rVert\to0}\sum_{j=1}^nf(\gamma(x_j^*))(\gamma(x_j)-\gamma(x_{j-1})),$$

where $\gamma:[a,b]\to\mathbb{C}$ is a curve. Let us assume that $\gamma$ is $C^1$. Then we have the expansion

$$\gamma(t)=\gamma(s)+\gamma'(s)(t-s)+R(t-s),$$

where $\frac{R(t-s)}{t-s}\to0$ as $t\to s$. Consequently

$$\gamma(x_j)-\gamma(x_{j-1})=\gamma'(x_{j-1})(x_j-x_{j-1})+R(x_j-x_{j-1}).$$

But then notice that

\begin{align*} \sum_{j=1}^nf(\gamma(x_j^*))(\gamma(x_j)-\gamma(x_{j-1})) &=\sum_{j=1}^nf(\gamma(x_j^*))(\gamma'(x_{j-1})(x_j-x_{j-1})+R(x_j-x_{j-1})) \\ &=\sum_{j=1}^nf(\gamma(x_j^*))\gamma'(x_{j-1})(x_j-x_{j-1})+\sum_{j=1}^nf(\gamma(x_j^*))R(x_j-x_{j-1}). \end{align*}

Notice how the first term in this sum looks an awful lot like a Riemann sum for the integral $\int_a^bf(\gamma(t))\gamma'(t)\,\mathrm{d}t$, the only difference being that we evaluate $f\circ\gamma$ and $\gamma'$ at different points in the subintervals of the partition. This is where the assumption of $\gamma$ being $C^1$ saves us. I will not go into the details, because my point is to give you the idea of why the definition you've seen makes sense, but one can now show that the second term also vanishes as the mesh of the partition goes to zero, and so one obtains that

$$\int_\gamma f(z)\,\mathrm{d}z=\lim_{\lVert\mathcal{P}\rVert\to0}\sum_{j=1}^nf(\gamma(x_j^*))(\gamma(x_j)-\gamma(x_{j-1}))=\underbrace{\lim_{\lVert\mathcal{P}\rVert\to0}\sum_{j=1}^nf(\gamma(x_j^*))\gamma'(x_{j-1})(x_j-x_{j-1})}_{=\int_a^bf(\gamma(t))\gamma'(t)\,\mathrm{d}t}+\underbrace{\lim_{\lVert\mathcal{P}\rVert\to0}\sum_{j=1}^nf(\gamma(x_j^*))R(x_j-x_{j-1})}_{=0}=\int_a^bf(\gamma(t))\gamma'(t)\,\mathrm{d}t,$$

and so you can see that, with this much more natural definition, analogous to what we do on the real line, we obtain the formula you have for sufficiently nice functions.

Answer 2

The (smooth directed) contour is parameterised by $z=\gamma(t)$ where $\gamma:\mathbb{R}\to\mathbb{C}$. Then the contour integral definition can be intuitively thought of as a simple case of substitution, where the differential term $dz=\gamma'(t)dt$. Which gives you your $$\int_Cf(z)dz=\int_a^bf(\gamma(t))\gamma'(t)dt$$ I'm glossing over some rigorosities, since it seems like you're more interested in the intuition.

---

Complex integration is completely analogous to the real-valued Riemann integral you're familiar with, in the sense that you partition the curve into elements, sum up the weighted function values, then take the limit as the elements become infinitesimally small. The difference is in the real-valued case, the "weights" are the lengths of the $\Delta x$ elements, but in the complex case the "weights" are the small complex numbers $\Delta z$.

This is probably why you read that there is no "geometric intepretation", because while $f(x)\Delta x$ are rectangles in the real-valued sum, there is no nice geometric representation of the complex-valued $f(z)\Delta z$.

---

Complex integrals are certainly similar to line integrals, which are$$\int_C f(\mathbf{r}) ds$$

Informally, $ds$ is the length of an infinitesmial element of the arc, which can be substituted for $$ds=|\mathbf{r}'(t)|dt$$given some parameterisation $\mathbf{r}(t)$.

The difference (again, informally) is the line integral integrates over infinitesimal real lengths $ds$, but the complex integral is over infinitesimal complex numbers $dz$.

Answer 3

Line Integral :

Let us say we have a Curve $\gamma$ from $a$ to $b$ like this :

Along the Curve $\gamma$ , we have some number we want to integrate. Eg We put some tar on the curvy road. At Point $r$ , we use $f(r)$ amount of tar where $ds$ is the road strip size. We want total tar used.
Naturally , we want to integrate over all such Points $r$ on Curve $\gamma$ :
$$\int_\gamma f(r) ds = \int_a^b f(r) ds$$

We do not know how to do that easily , we do know Definite Integration. Hence we want to put it on a linear line such that at Point $t$ , we get the Point on the Curve $r(t)$ & then Integrate over $t$. It is just the usual change of variables , nothing more to it. It introduces the term $r'(t)dt$ in place of $ds$
$$\int_a^b f(r(t)) r'(t)dt$$
It will look some thing like this :

We can also see that when curve moves forwards , eg at $t_1$ , $r'(t)$ is Positive , while when curve moves backwards , eg at $t_2$ , $r'(t)$ is Negative : It will make the Integral add the tar amount & subtract the tar amount depending on the Sign. We do not want that : We always want to add. Hence , we introduce "absolute value" to eliminate Negative values.
$$\int_\gamma f(r) ds = \int_a^b f(r(t)) |r'(t)|dt$$

Contour Integral :

Situation is same , except that the value we want to integrate over are all Complex numbers. There is no Concept of Positive or Negative now.

At Point $z$ on the Curve $\gamma$ having tiny strip $dz$ , we have some number $f(z)$.
$$\int_\gamma f(r) dz = \int_a^b f(z) dz$$
We do not know how to get that , hence we introduce Parameter $t$ to convert to linear line.
Point $t$ with the usual change or variables is on the linear line , which corresponds to the tiny strip $z'(t)dt$ at the Point $z(t)$ on the Curve.
$$\int_\gamma f(r) dz = \int_a^b f(z(t)) z'(t)dt$$
It will look like the Definite Integral given earlier , except that the function will have Complex values.
Here , we general want to add & subtract (Eg Current or force or magnetism) the values , hence we do not use $|z'(t)|$.

SUMMARY :

In Line Integral , $r$ moves along the curvy line.
With Change of variables , $t$ moves from real number $0$ to $1$ to match $a$ & $r$ & $b$ on the Curve.
In Contour Integral , $z$ moves along the curvy Contour.
With Change of variables , $t$ moves from real number $0$ to $1$ to match $a$ & $z$ & $b$ on the Contour.

Answer 4

Let $f$ be holomorphic. The key point (which was somehow missed in the other answers) is that the integral is there to calculate an antiderivative. Let's say you are at the point $z=\gamma(x)$ and want to calculate an antiderivative $F$ at the point $z+dz=\gamma(x+dx)=\gamma(x)+\gamma'(x)dx$. The antiderivative by definition should satisfy $$F(z+dz)-F(z)=f(z)dz=f(\gamma(x))\gamma'(x)dx.$$ To make the point more clear let's look of what happens when $\gamma(x)$ goes up, i.e. when let's say $\gamma'(x)=i$. Now what should $F(\gamma(x+dx))$ be? If one sets it naivly to $F(\gamma(x))+f(\gamma(x))dx$ the derivative (if it would exist, of course it doesn't with such a flawed definition) of $F$ at $\gamma(x)$ would have to be $\frac{f(\gamma(x))}{i}$, not $f(\gamma(x))$ as wished for. This explains the phase, the magnitude should be self explanatory.

The integral will be $F(b)-F(a)$ where $a$ and $b$ are the end points of the contour (but be careful in case the antiderivative $F$ is multivalued because then you have to use the correct branches for example $\int_{S^1}1/zdz=\log(1)-\log(1)$ but the left $\log$ is "one branch higher" than the right one so differs from the right one by $2\pi i$ (this is logically kinda circular but one (of many) very useful way(s) to think about things)).