Prove that $M$ is the centroid of the triangle $BCD$.

Question

the question

Consider the tetrahedron $ABCD$ and $M$ a point inside the triangle $BCD$. Parallels taken from $M$ to the edges $AB$, $AC$, $AD$ intersect the faces $(ACD)$, $(ABD)$, respectively, $(ABC)$ at the points $A', B',$ respectively, $ C'$. If $(BCD) || (A' B 'C')$ , prove that $M$ is the centroid of the triangle $BCD$.

my idea

the drawing

So we have $B'M|| AC, A'M||AB, C'M||AD$

As you can see, I intersected the plane $(A'B'C')$ with $AD,AC,AB$ in $X,Y,Z$

We can simply demonstrate that $Y,A',X$ are collinear Analogus, $X,B',Z$ and $Z,C',Y$ are collinear

We can demonstrate that because $(ZYX)||(BCD)$ and both planes are intersected by 2 parallel lines such as BZ and A'M , we get that BZ=A'M which makes BMA'Z a parallelogram

Analogus, XC'MD and YB'MC parallelograms.

I don't know what to do going forward! Hope one of you can help me! Thank you!

Answer 1

Let M be centroid of BCD, consider plane ABE where E is middle of CD, because MA’ is parallel to AB and shares point M with plane ABE, it lies in plane ABE and thus A’ lies in plane ABE, ratio A’E/AE is the same as ratio ME/BE, which is 1/3 because M is centroid of BCD, it follows that A’ is also centroid of ADC, same holds for B’ and C’ – they are centroids of faces ABD and ABC, in other words in any tetrahedron line connecting centroids of two faces is parallel to the only rib which is not a side of both those faces. Centroids A’, B’, C’ share the same distance from plane BCD – 1/3 of distance from plane BCD to A and planes A’B’C’ and BCD are parallel.

If M is not centroid of BCD, we have situation described in my picture, where lines KO, LP, NQ are lines parallel to sides of BCD through S – centroid of BCD. If M is closer to side CD then line KO, then A’ will be lower then 1/3 of height of A over plane BCD, if farther, then A’ is higher then 1/3 of height of A. Similar relations hold for heights of B’,C’ and position of M relative to lines LP, NQ. As we can see, M cannot be simultaneously closer to sides BC, BD, DC then all three lines KO, LP, NQ (three corresponding strips share in common only S), and thus, A’, B’, C’ cannot be simultaneously lower then 1/3 of height of A over plane BCD. Also M cannot be simultaneously farther from sides BC, BD, DC then all three lines KO, LP, NQ (three corresponding triangles share in common only S), and thus, A’, B’, C’ cannot be simultaneously higher then 1/3 of height of A over plane BCD. This implies that at least one point out of A’, B’, C’ is higher and at least one is lower, this means that plane A’B’C’ is not parallel to BCD. We proved that plane A’B’C’ is parallel to BCD iff M is centroid of BCD.

Answer 2

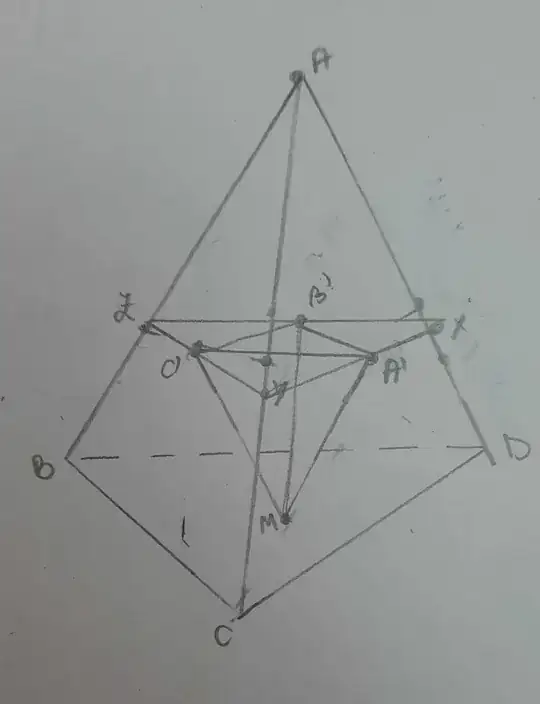
This answer uses $X,Y,Z$ that you defined.

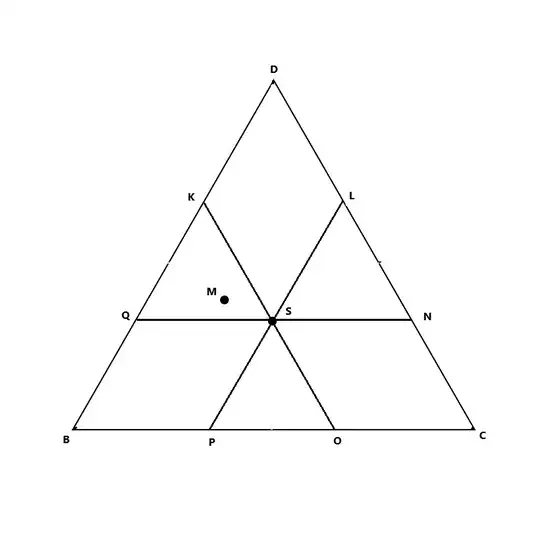
Let $E$ be a point on $BC$ such that $ME\parallel CD$.

Let $F$ be a point on $CD$ such that $MF\parallel BD$.

Let $G$ be a point on $BD$ such that $MG\parallel BC$.

Then, we have $$AD:AX=BC:BE\tag1$$ (Proof : Let us consider the plane $\alpha$ on which $A,A',B$ and $M$ exist. Let $P$ be the intersection point of $\alpha$ with $CD$. Then, we have $PA:AA'=PB:MB$. We also have $PA:AA'=AD:AX$ and $PB:MB=BC:BE$. So, we get $AD:AX=BC:BE$.$\ \square$)

Similarly, we have $$AD:AX=CD:CF\tag2$$ $$AC:AY=DB:DG\tag3$$

Now, if $(BCD)\parallel (A'B'C')$, then we can say that $AD:AX=AC:AY$.

So, it follows from $(1)(2)(3)$ that $$BC:BE=CD:CF=DB:DG\tag4$$

Let $H$ be a point on $BD$ such that $MH\parallel CD$.

Let $I$ be a point on $BC$ such that $MI\parallel BD$.

Let $J$ be a point on $CD$ such that $MJ\parallel BC$.

We have $$CJ=FD\tag5$$

By Menelaus's theorem, we get $$\frac{CF}{FP}\times\frac{PM}{MB}\times\frac{BI}{IC}=1$$ Since $\frac{BI}{IC}=\frac{DF}{CF}$, we have $$\frac{PM}{MB}=\frac{FP}{DF}\tag6$$

By Menelaus's theorem, we get $$\frac{DJ}{JP}\times\frac{PM}{MB}\times\frac{BG}{GD}=1$$ Since $\frac{BG}{GD}=\frac{CJ}{JD}$, we have $$\frac{PM}{MB}=\frac{JP}{CJ}\tag7$$

It follows from $(5)(6)(7)$ that $$JP=FP\tag8$$

It follows from $(5)(8)$ that $P$ is the midpoint of $CD$.

Similarly, we can see that the intersection point of $CM$ with $BD$ is the midpoint of $BD$.

Therefore, we can say that $M$ is the centroid of the triangle $BCD$.

---

Added :

how do you know in the first proof that $P$ is collinear with $A,A'$ and $B,M$? How do you know that the intersection of $AA'$ with $BM$ is point $P$ which is on $CD$?

Since $A'M\parallel AB$, the line $AA'$ intersects the line $BM$. Let $Q$ be the intersection point of $AA'$ with $BM$. We see that $Q$ is on $\alpha$. We also see that $Q$ is both on the plane $ACD$ and on the plane $BCD$. So, we see that $Q$ is on the line $CD$. It follows that $P=Q$. So, $P$ is both on the line $AA'$ and on the line $BM$.

I read what you wrote forward and saw that you dont think that $BM$ interesects $AA'$ in point $P$

I replaced $K$ with $P$ since $K$ is nothing but $P$.

Can you please explain how you got the following ratios $PA:AA′=PB:MB, PA:AA′=AD:AX$ and $PB:MB=BC:BE$

• $PA:AA′=PB:MB$ since $\triangle{PAB}\sim\triangle{PA'M}$.

• $PA:AA′=AD:AX$ since $\triangle{AA'X}\sim\triangle{APD}$.

• $PB:MB=BC:BE$ since $\triangle{BME}\sim\triangle{BPC}$.

Answer 3

The question cried for a vector approach so loudly, that I could not resist it.

Let the vertex $A$ is placed at the origin of the space. Since $M$ is inside the triangle $BCD$, $M$ is a convex combination of $B$, $C$, and $D$. That is, there exist nonnegative numbers $\lambda_B$, $\lambda_C$, and $\lambda_D$ such that $\lambda_B+\lambda_C+\lambda_D=1$ and $M=\lambda_B B+\lambda_C C+\lambda_D D$. Parallels taken from $M$ to the edges $AB$, $AC$, and $AD$, respectively, intersect the faces $(ACD)$, $(ABD)$, and $(ABC)$, respectively, at the points $\lambda_C C+\lambda_D D$, $\lambda_B B+\lambda_D D$, and $\lambda_B B+\lambda_C C$, respectively. The parallelity of the respective planes implies that they have a common normal vector, say, $E$. Then we have the following equalities for the inner products $$(E,B)=(E,C)=(E,D)\ne 0$$ $$(E,\lambda_C C+\lambda_D D)=(E,\lambda_B B+\lambda_D D)=(E,\lambda_B B+\lambda_C C).$$ It follows $$\lambda_C+\lambda_D=\lambda_B+\lambda_D=\lambda_B +\lambda_C,$$ $$\lambda_B=\lambda_C=\lambda_D=\frac 13,\mbox{ QED.}$$