Closed form for $\int_0^{\pi/2}\arctan\left(\frac12\sin x\right)\mathrm dx$?

Question

Is there a closed form for $I=\int_0^{\pi/2}\arctan\left(\frac12\sin x\right)\mathrm dx$ ?

Context

Earlier I asked "Find the area of the region enclosed by $\frac{\sin x}{\sin y}=\frac{\sin x+\sin y}{\sin(x+y)}$ and the $x$-axis".

The answer turned out to be $\frac{\pi^2}{8}$, but the proof is non-trivial.

A natural follow-up question is, what happens if we change all the sines to tangents?

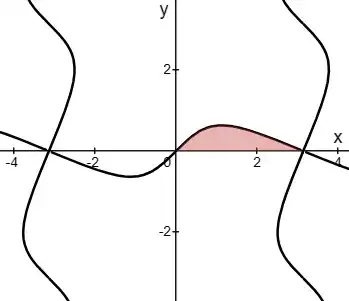
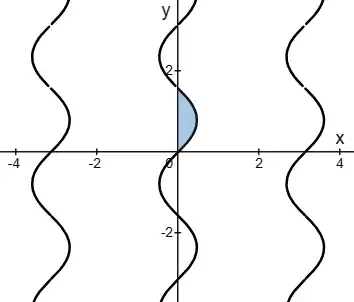
So what is the area of the region enclosed by $\frac{\tan x}{\tan y}=\frac{\tan x+\tan y}{\tan (x+y)}$ and the $y$-axis, from $y=0$ to $y=\frac{\pi}{2}$ ?

To make the algebra easier, we swap $x$ and $y$, and seek the area enclosed by the new graph and the $x$-axis. Letting $X=\tan x$ and $Y=\tan y$, we have $X\left(\frac{X+Y}{1-XY}\right)=XY+Y^2$. Solving the quadratic in $Y$ gives $y=\arctan\left(\frac12\sin 2x\right)$.

So the area is $\int_0^{\pi/2}\arctan\left(\frac12\sin 2x\right)\mathrm dx$, which equals $\int_0^{\pi/2}\arctan\left(\frac12\sin x\right)\mathrm dx$ due to symmetry.

My attempt

I found that $\int_{0}^{\pi/2}\arctan(\sin(x))dx=\frac{\pi^2}{8}-\frac{\ln^2(\sqrt{2}-1)}{2}$. I tried to use this method, but it doesn't seem to work, because in my integral there is a $\frac12$, which is not equal to its reciprocal.

Answer 1

\begin{align} \int_0^{\pi/2}&\tan^{-1}\frac{\sin x}2dx =\int_0^{\pi/2}\int_0^{\frac12} \frac {\sin x}{1+y^2 \sin^2x}dy \ dx\\ &=\int_0^{\frac12} \frac {\sinh^{-1}y}{y \sqrt{1+y^2}} {dy}\overset{\sinh^{-1}y=\ln\frac{1+t}{1-t}}= \int^{\phi^{-3}}_0\frac{\ln \frac{1+t}{1-t}}{t}dt \\ &=\text{Li}_2(\phi^{-3}) - \text{Li}_2(-\phi^{-3}) = \frac{\pi^2}{12}-\frac32 \ln^2 \phi \end{align}

Answer 2

The antiderivative is very complicated but using the bounds $$I=\int_0^{\frac \pi 2}\arctan\left(\frac{\sin (x)}2\right)\mathrm dx=\frac{1}{12} \left(\pi ^2-6 \sinh ^{-1}(2)\,\, \text{csch}^{-1}(2)\right)$$

If you use series $$\arctan\left(\frac{\sin (x)}2\right)=\sum_{n=0}^\infty (-1)^n \,\frac{ \sin ^{2 n+1}(x)}{2^{2 n+1}\,(2 n+1)}$$ you should get the same result simplifying $$I=\frac{1}{2} \, _3F_2\left(\frac{1}{2},1,1;\frac{3}{2},\frac{3}{2};-\frac{1}{4}\right)$$ which is the result of $$\sum_{n=0}^\infty (-1)^n \,\frac{\sqrt{\pi }\,\, \Gamma (n+1)}{2^{2 n+1}\,(2 n+1) \Gamma\left(n+\frac{3}{2}\right)}$$

Answer 3

Partial answer

$$ I(a)=\int_0^{\pi/2}\tan^{-1}\left(a\sin(x)\right)\;dx\implies I'(a)=\int_0^{\pi/2}\frac{\sin(x)}{{1+a^2\sin^2x}}dx=\int_0^{\pi /2}\frac{\sin x}{1+a^2-a^2\cos^2(x)}dx$$ Letting $t=\cos (x)$: $$ \int_0^{1} \frac{dt}{1+a^2-a^2t^2}=^{v=iat}(ai)^{-1}\int_0^{ai}\frac{dv}{1+a^2+v^2}=(a)^{-1}\left(\frac{1}{1+a^2}\tanh^{-1}({a\over1+a^2})\right) $$ So we have: $$ I(a) = \int \frac{1}{a(1+a^2)}\tanh^{-1}\left(\frac{a}{1+a^2}\right)da $$