Checking KKT Constraint Qualifications

Question

When checking whether the CQ are satisfied in KKT, i.e. checking for Linear Independence amongst all combinations of the constraints.

Is it true to say we only need to check combinations that could be simultaneously effective (binding)? So if two constraints can't bind at the same time i.e. they would create the empty set, i don't need to check their gradient vectors for Liner Dependence?

This seems to be the case but i recently came across the following in a mark scheme, i'm struggling to interpret it, and wondered if it was stating the above but only for mixed constraint problems.

For mixed constraint problems, we follow the same approach as for inequality constraint optimisation problems, but we can restrict our attention to just those combinations of effective constraints that include the equality constraints.

I would also appreciate some intuition as to why the importance of Linear Dependence in the context of KKT constraints is I feel like the Lagrange/KKT solutions wouldn't know how to allocate tangent points if multiple constraints were LD - somewhat analogous to how regression fails with perfect collinearity of regressors? Thanks!

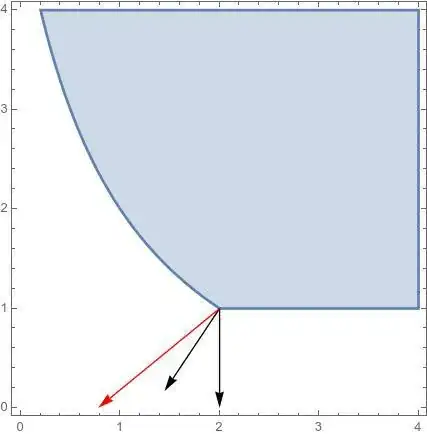
Example

Taking the example in the image below:

• I would state that the CQ holds for $h_1, h_3$ because if $h_1$ is binding $x = 0$ which implies $y=5$, which creates vectors $(0,1)$ and $(6,1)$ which are LI.

• Their approach is always the other way round. They say for $h_1$ and $h_3$ to be LD, then $x = -1$ this violates the constraint $h_1$

Are both approaches valid? Does my approach of starting with the implications of the constraints being binding run into any problems, compared with starting with the implications of the constraints being LI.

Answer 1

Assuming that the problem is a minimization one, We have in light blue, the feasible region, and in black the gradients of the actuating restrictions at the point $(2,1)$. In red, the objective function gradient. The KKT criterion translates geometrically into knowing whether $\nabla f(x,y)$ is trapped in the positive cone generated by the actuating constraints gradients. As we can observe, $\nabla f$ is out of the positive cone, hence $(2,1)$ is not a minimum point. Having in mind this setup, we can handle conveniently the sense of restriction gradients. In the figure we have represented $-\nabla h_2(2,1)$ and $-\nabla h_3(2,1)$ as well as $-\nabla f(2,1)$.

Answer 2

Your intuition and interpretation are on the right path. In optimization problems with constraints, understanding which constraints are likely to bind together and ensuring these constraints' gradients are linearly independent is crucial for correctly applying the KKT conditions and for the stability and uniqueness of the solution (When multiple constraints' gradients are linearly dependent, there can be an issue in determining unique values for the Lagrange multipliers. This is analogous to the problem in regression known as multicollinearity, where collinear predictors prevent unique or stable estimation of regression coefficients).

The quote you gave indicates that in problems involving both equality and inequality constraints, priority is given to equality constraints when determining which sets of constraints to consider. This is because equality constraints must always be binding at any feasible solution, thus defining part of the feasible region's boundary by default. In contrast, inequality constraints may or may not be binding. Thus, the focus is shifted to combinations where the essential (always-binding) equality constraints are included, and only relevant inequality constraints that might be binding are considered in conjunction.

Answer 3

I read your question and comments several times to hopefully understand your concern.

You should note that the CQ (of a certain type) needs to be checked at each point, not for constraints. For example, we say the LI CQ holds at some point $x$, not for constraints $g(x)\le 0$.

To check the LI CQ, you should first find all feasible points on which some constraints are active because other points satisfy the LI CQ. Hence,

• If you have at least one equality constraint, then all feasible points need to be checked.
• If you have only inequality constraints in your model, only those points on which some constraints are active need to be checked. Thus, in this case, you need to determine those points first, and then check the LI CQ at each of them.

Regarding your last question: Checking some CQ condition is required for using KKT conditions as necessary conditions for optimal solutions because there are optimization problems whose optimal solutions do not satisfy KKT conditions (see here for an example).

My final point: To get rid of checking CQ conditions when it becoms difficult to check them, you can use FJ optimality conditions that requires no CQ condition checking (they reduce to KKT when some CQ holds at all feasible points).