3

A line with equation $L = (1, 0, -2) + s(2, -1, 2)$ intersects with the plane $x + 2y + z = 2 $ at an angle of $\theta$ degrees.

I am having some difficulty understanding why the dot product is necessary and why I cannot simply obtain $\theta$ by using the right-angled triangle formed between the direction vector of the line and the normal vector to the plane i.e., $\theta=\arcsin\frac{\sqrt{1^2+2^2+1^2}}{\sqrt{2^2+1^2+2^2}}$

Apologies for the rudimentary question, thanks in advance.

sesandc3123
  • 67
  • This is not a right triangle! catheder and hypothenuse the same length? – trula Apr 17 '24 at 17:28
  • They are not the same length; the cathetus is $\sqrt{6}$ and the hypotenuse is $\sqrt{9}$ – sesandc3123 Apr 17 '24 at 17:45
  • Your approach is the similar to dot product. You used the angle between the normal and the line direction with sinusoidal in triangular whereas dot product use the cosine. Note in your approach, you'd better make sure the line vector starts from the plane. – MathArt Apr 17 '24 at 18:45

1 Answers1

4

In your approach you do not have a right-angled triangle:

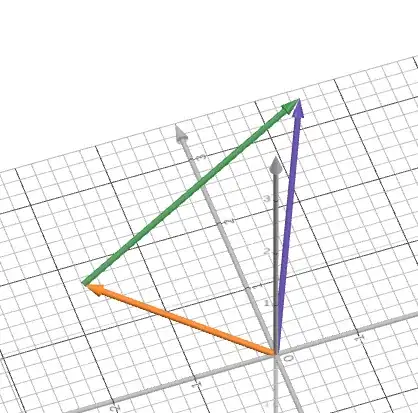
enter image description here

where the purple is the normal vector and orange the direction vector. Here's a link to the desmos

So using sin here doesn't make any sense because you don't have a right angle triangle, if it was right angle, then sure but it's not.

Before continuing first at least convince yourself why there is a cosine in the dot product equation.

Now at the same time think about the dot product equation:

\begin{align*} \langle x,y\rangle = \|x\|\|y\|\cos(\theta) \end{align*}

and let's make it look more like what you wrote that is:

\begin{align*} \arccos\left(\frac{\langle x,y\rangle}{\|x\|\|y\|}\right) = \theta \end{align*}

Note that this directly provides a solution using the dot product, but let's see if we can make your approach work.

We could try and force a right angle, by scaling our direction vector, like this: enter image description here

And then your equation would work, where we instead use the length of this scaled direction vector. But in order to do that we would need to determine what the scaling factor is.

What you'd be looking for is actually the projection of the normal vector onto the direction vector, and can be thought of as the closest vector in the direction of d which is closest to the tip of n, or that it makes a right angle with it.

Either way you've produced a new problem which seems just as hard as your initial one. And usually we deduce the projection by setting up an equation where a dot product must equal 0, and finding that:

$$proj_\vec{b}(\vec{a})=\frac{\vec{a}\cdot \vec{b}}{\vec{b}\cdot \vec{b}}\vec{b}$$

In closing out, you ask why it is necessary to use the dot product, with your approach using it allows us to find the projection which you can then use your idea to find the angle between the two vectors, alternately we can use the equation I stated in the aside on the dot product.

If you wanted to do this without dot product at all, you would have to find a way to determine the scaling factor without a dot product and then follow your approach. (Which I do not know how to do)

cuppajoeman
  • 404