15

N.B. - I'm looking for the simplest way to ascertain the number of templates $T$ (see below) comprising the structure from just one angle alone; that is, I'm sitting down looking up at this thing, and I want a way to compute its cardinality based on the simplest methods, but perhaps relying on some underlying abstract concept, in particular, graph theory, geodesics, topology, algebra, or something totally new.

My working theory is that we need only the equation

$$V-E+F=2,$$

and the Inclusion-Exclusion Principle. In fact, we might also need the fact that the star is a fraction of the whole, and some other symmetry to rely on to create a system of equations. That is

$$\frac{V}{n}-\frac{E}{n}+\frac{F}{n}=2$$

and

$$\frac{V}{m}-\frac{E}{m}+\frac{F}{m}=2,$$

where we know the relationship between $m$ and $n$. Actually, that makes no sense... Hmm...

UPDATE: I have verified, with sufficient effort, Mr. Narain's proposal that the structure is a snub dodecahedron:

enter image description here

There are indeed 60 pieces, however, I'd still like a lazy method using the ideas I've alluded to all throughout this post...

I'm at a fancy restaurant, and I saw these template ball lights:

enter image description here http://tinypic.com/r/2co6b9w/5

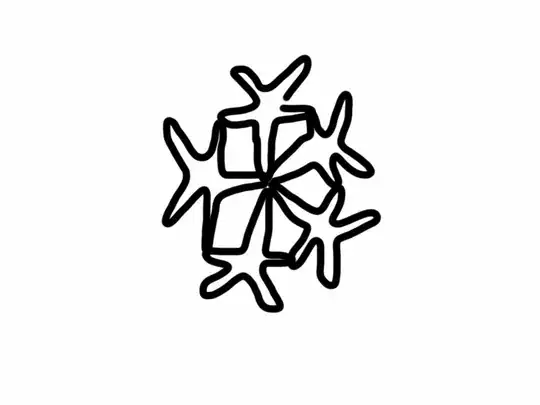
I'm trying to figure out the number of template pieces, call them $T$; they look like this:

enter image description here http://tinypic.com/r/29cs8cw/5

Here is my approach: Count the number of things that look like this:

enter image description here http://tinypic.com/r/wmnssn/5

Now notice that for each $T$ coming out from the center there are four legs which the rest are connected to, two of which are connected to adjacent $T$'s which are coming out from the same center mentioned before. I feel this problem is one of algebra. My friend here thinks that if you measured the shape of $T$, then you could find it easily with the surface area of a sphere, but she can't seem to work out how to get the number of $T$'s. If you need more photos, let me know.

Just in case you don't see it:

enter image description here

This appears to be a snub dodecahedron--as was pointed out by one of the commenters--and can be seen in an overlay here:

enter image description here

Look at this:

enter image description here

I believe these two can be related in a system of equations via the Euler Characteristic--perhaps I'd need a third distinct shape...

Here are some statistics:

enter image description here

Based on these statistics, here is the template--just in case you want to make one for yourself:

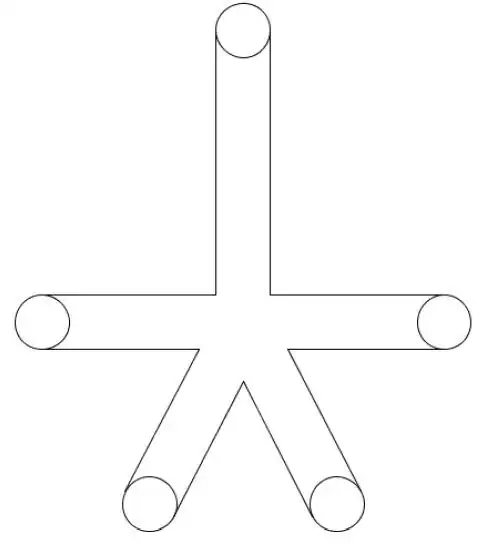
enter image description here

If you pay me $50 I'll make a larger one for you out of balsa wood. ^_^

THE BIG IDEA:

Assume I am a tree--maybe I'm an African Baobab, and my Baobab friend next to me has this thing dangling motionlessly from her branches. Me being an Baobab, I don't know about snub dodecahedrons, but--for some genetically mutative reason--I know a bit of mathematics. So, now, I'm looking at this thing wondering if I can count how many $T$'s there are (see above) just by noting how the arms of the $T$'s are connected. What is the least amount of data that I need from my single, grounded point of view to ascertain the number of the $T$'s comprising this object?

Trancot
  • 4,127
  • What theory should be applied here? How do I define "ballness," as it were? – Trancot Nov 06 '13 at 00:10
  • Maybe we could be more Tao Te Ching and just focus on the empty space. There are six holes in the center, then fifteen holes surrounding the main star, and so on... – Trancot Nov 06 '13 at 00:20
  • Or perhaps we should consider the degree of the vertices. There appear to be three types; one has degree five, one has degree four, and one has degree three. – Trancot Nov 06 '13 at 00:22
  • A diagram would be very nice if you included it in your analysis. – Trancot Nov 06 '13 at 00:55
  • This may sound complicated, but can anything be extracted from the dual graph of sub-region of a map that happens to be a fraction of of a sphere--in this case the star? – Trancot Nov 06 '13 at 02:09
  • I think I've made a discovery! The center vertex has degree 5, moving outward to the next vertex--the center of the $T$--we have four paths to choose from assuming we can't go back, and after this we have two choices. So that's 5, then 4, then 2. Those numbers seem important... – Trancot Nov 06 '13 at 02:38
  • When I said "one has degree four" just forget that because there are actually just two types with degree 5... – Trancot Nov 06 '13 at 02:42
  • I'm pretty sure those things you outlined in green are arranged like the pentagons in a snub dodecahedron. See: https://i.sstatic.net/2XbU2.jpg. There are $12$ pentagons, each of which is made of $5$ pieces, so there are $60$ pieces in total. –  Nov 06 '13 at 05:05
  • That seems very convincing... Hmm... My friend thinks otherwise--empirically... She says there were certainly 8, but then again... Can you make an overlay of the two images? I'm going to try to make an overlay in GIMP. – Trancot Nov 06 '13 at 05:32
  • So what you're saying is that apart from the six visible in the front of the ball there are only two in the back. –  Nov 06 '13 at 05:54
  • No. My friend is. I say it's convincing. Actually, I'm on board. See my most recent edit, @RahulNarain. – Trancot Nov 06 '13 at 06:00
  • Hey, @RahulNarain, if you make the $T$--to the correct dimensions, I'll print 60 of them out, cut them out, and then assemble them to see if you're right. What do you say? – Trancot Nov 06 '13 at 06:16
  • I'll also give you the +100--if you submit an answer--for giving the most insightful answer thus far. – Trancot Nov 06 '13 at 06:19
  • There is the truncated icosahedron with 12 pentagonal and 20 hexagonal faces-the shape of a soccer ball. The vertices of the pentagons point towards each other, while on the snub dodecahedron the edges of the pentagons are parallel. Neither is really true in this model, but I think the first is closer. – Ross Millikan Nov 06 '13 at 14:16
  • Does anybody here know how to project a snub dodecahedron from the sphere onto the plane? – Trancot Nov 06 '13 at 20:46

3 Answers3

2

One approach is to use the surface area of the sphere. If you wrap a tape measure around the sphere you can get the circumference and hence the radius $R$. The surface area is $4\pi R^2$. Now straighten out in your mind the edges of your shape and measure its area. Divide that into the area of the sphere and you have it. You don't have to be that precise, as you are trying to tell the difference between $8$ and $9$, so you need $10\%$ accuracy, which isn't hard.

Another approach is to try to determine the geometry of the ball. The ring of arms of your group of five looks like a pentagon to me. If the pattern looks the same at each juncture, it would be a dodecahedron, which has $12$ pentagons. This pentagon uses $\frac 25$ of each template (it uses one arm and shares two other arms with the neighboring pentagon), so you should need $\frac 52 \cdot 12=30$ templates. I suspect that there are other styles of vertex than three pentagons. If you can define what meets at each vertex, you can get the number of arms. The Euler characteristic formula can help here.

A more practical approach is to put a white dot at the center of each piece and count them.

Ross Millikan
  • 383,099
  • Yes, which is the initial conclusion I came to vis a vis your last comment; however, I'm lazy, remember? Therefore, I have no way of practically computing such things. I'm looking for an answer that is so brilliant it could be explained to a child. Much in the spirit of Einstein, I'd like a sort of "If you can't explain it to a six year old" kind of approach to the problem using algebra and... well... something else. – Trancot Nov 06 '13 at 00:48
  • All the six year olds I know can count to $40$. That many Post-its they can understand. – Ross Millikan Nov 06 '13 at 03:45
  • I'm lost... Post-its? – Trancot Nov 06 '13 at 04:16
  • I would use Post-it notes to identify the centers, then take them off and count. – Ross Millikan Nov 06 '13 at 14:07
2

$N$ stick figures. Belly vertices: $N$. Hands and feet vertices: $4N/3$. Head vertices: $N/5$. Sticks (arms, legs, neck): $5N$. Open spaces: $5N/2$.

$$\left(N + \frac{4N}{3} + \frac{N}{5}\right) - (5N) + \left(\frac{5N}{2}\right) = 2.$$

$$\frac{N}{30}=2.$$ So $60$ stick figures in total.

WimC
  • 33,414
  • 2
  • 52
  • 98
  • That's about what I have here on paper. Good! Maybe you wouldn't mind explaining to the audience, in particular, why is $V$, $E$ and $F$ this way, and so on. Explain your technique/approach--if you wouldn't mind. – Trancot Nov 06 '13 at 21:05
  • Best answer! Bravo! – Trancot Nov 06 '13 at 21:11
1

Let $R$ be the ball's radius. Let's go really lazy and just use the picture. The apparent diameter of the piece with the green outline is roughly $2/3$ of the apparent diameter of the ball. So is its radius, it's $2R/3$. It's apparent area of the piece is the n $4\pi R^2/9$ (approximated as a flat disk) and the apparent area of the spherical ball is $4\pi R^2$, dividing the spherical area with the piece's area is exactly 9. However, the piece is actually a spherical cap so it's area is larger than what's apparent but not by much. Therefore the answer should be less than 9. We get 8 such pieces.

Alexander Vlasev
  • 3,170
  • What I'm really looking for is an answer that uses the vertices, their respective degrees, and the architecture of how they're connected, to come to an even quicker answer. I'm not looking for a geometrically approximating approach, but something more reliant on topology, graph theory, and algebra--and perhaps something I've never even heard of. – Trancot Nov 06 '13 at 01:20
  • Are you sure you are not moving the goal-posts? Your comment on Ross's answer speaks of a brilliant answer that could be explained to a child. On my answer you wrote you want something more reliant on topology, graph theory, etc, or even something you've never heard of. You are making the constraints extremely tight. – Alexander Vlasev Nov 06 '13 at 01:28
  • Is there not a simple way to count the concentric holes that are generated outward from the center? Namely, the middle has 5, then the next ring has 15, and so on. – Trancot Nov 06 '13 at 01:28
  • Any such counting will lead you to something more complicated than just counting the number of pieces. Your friend's approach with measuring the area and all that is more practical and simpler. It's more so in the spirit of Fermi problems in general where you easily estimate some quantity to get a ball-park figure. In this case it gives you the right answer within a few lines of reasoning – Alexander Vlasev Nov 06 '13 at 01:32
  • Exactly correct, in my opinion topology and graph theory are just labels for very human ways of interpreting things. Children understand topology and graph theory at an intuitive level. The theory might, to us, seem abstract at first, but in my experience topological things are easier to explain to a child--of course, with sufficient thought. You can tell them there are 3 things coming out of this point, and there are 4 things coming out here, and they are all connected like this, so... Does that make sense? Have I won you over? Are you on my side now? – Trancot Nov 06 '13 at 01:32
  • I hear you Mr. Vlasev, but I'm holding out for something better. – Trancot Nov 06 '13 at 01:33
  • From your question: "N.B. - I'm looking for the simplest way to ascertain the number of templates T (see below) comprising the structure from just one angle alone; that is, I'm sitting down looking up at this thing, and I want a way to compute its cardinality based on the simplest methods, but perhaps relying on some underlying abstract concept."

    Ross's answer and mine are in line with what you asked whereas my approach is even simpler since you don't even need to measure anything (you just need to eyeball it). That said, I hope you find the kind of solution you are looking for.

     – Alexander Vlasev Nov 06 '13 at 01:36
  • That may be the case, but look at my tags. Would you like me to edit my N.B. comment? – Trancot Nov 06 '13 at 01:38
  • Both the methods suggested thus far don't--in my immediate opinion--seem practical enough to gauge the cardinality. What if I go into another fancy restaurant and find a ball with different vertex types with accompanying different degrees--not to mention different connectedness architecture. Silver bullet... That's what I'm looking for. What if the templates look like this: $Y$ How then would I calculat the cardinality? I can't feasibly just look up and say "Oh, that star looks like it's about $\frac{x}{y}$ths of the diameter, so it must be that there are $n$ such stars." – Trancot Nov 06 '13 at 01:43
  • I appreciate you answer--and Mr. Millikan's. In fact, I'd say, it's more in the spirit of Lawrence Weinstein's Guesstimaiton 2.0. – Trancot Nov 06 '13 at 01:47
  • Maybe that will be a more fruitful line of discussion for you: what sorts of things do you think you could reasonably look up and see immediately. For me it's easier or at least no harder to guess the fraction of the whole than it is to find a graph structure with easily computed degrees; I guess we differ in this respect. Is there any other measurement you think you could get in your desired time window? – Eric Stucky Nov 06 '13 at 01:49
  • Yes, as I've mentioned--don't you hate it when people say that--vertex degree, and whatever is meant by "connectedness architecture." I think when I say "connectedness architecture" I'm making an expression that is vague enough to leave the reader open to interpret it in any way, as, for example, it could mean--in this particular case--there is a pentagon, those templates have five arms, four of the arms are only touching two other arms of other templates, etc. – Trancot Nov 06 '13 at 01:59
  • I'm leafing through Prasolov's Intuitive Topology thinking I'm going to get an idea. – Trancot Nov 06 '13 at 02:01
  • If you know the pattern, then could you reproduce a projection of the pattern on the sphere onto paper? – Trancot Nov 06 '13 at 02:15
  • Well, one thing I COULD tell you is that the connectedness inside the green outline does not matter since only the connections between the green outline and the outside matter. If they are all the same shape connected in some way, the insides of each shape could look like anything. Perhaps a graph-theoretic approach can say a lot about how you can vary the connections between the green outline shapes. That is, if you change it a bit here, you'll have to change it here here and here which will give you some invariant. – Alexander Vlasev Nov 06 '13 at 02:49