Where is the error in evaluating this integration? :$\int_0^{\frac{\pi}{2}} \frac{dx}{\cos(x)+\sin(x)}$

Question

Where is the error in evaluating this integration? :$$\int_0^{\frac{\pi}{2}} \frac{dx}{\cos(x)+\sin(x)}$$ let: $ u=\sin(x)+\cos(x)$ this implies $u^2=1+\sin(2x)\implies dx=\frac{u}{\sqrt{2u-u^2}}du$ therfore: $$I=\int_0^{\frac{\pi}{2}} \frac{dx}{\cos(x)+\sin(x)}=\int^1_1\frac{du}{\sqrt{2u-u^2}}=0$$

But Using Wolfram alpha then $I=\sqrt{2}\tanh^{-1}\left({\frac{1}{\sqrt{2}}}\right)$

Answer 1

Let $u=\sin x-\cos x$ instead $$\int_0^{\frac{\pi}{2}} \frac{dx}{\cos x+\sin x}=\int_0^{\frac{\pi}{2}} \frac{\sin x+\cos x}{(\cos x+\sin x)^2}dx\\ = \int_{-1}^{1} \frac{du}{2-u^2}={\sqrt2}\tanh^{-1}\frac 1{\sqrt2} $$

Answer 2

Will Jagy's comment hits the nail on the head. Your substitution is not injective. See the plot of $u(x)=\cos x+\sin x$ on $0\le x\le \dfrac\pi2$:

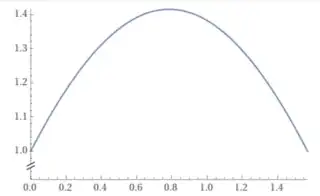
In order to use this substitution, you need to first split up the integral at $x=\dfrac\pi4$. You must be careful when reversing the substitution, however, because there are infinitely many $x$ that satisfy the equation for a given $u$:

$$u = \cos x + \sin x = \sqrt2\,\sin\left(x+\frac\pi4\right) \\ \implies x + \frac\pi4 = \color{red}{\pm} \arcsin\frac u{\sqrt2} + \color{red}{2n\pi} \\ \implies dx = \color{red}{\pm}\frac{du}{\sqrt{2-u^2}}$$

Note that you've also made a small mistake in computing and subsequently replacing $dx$ in the $u$-integral.

When solving for the limits in the $u$-integral, you need to choose the correct branch of $\arcsin$ depending on the domain of $x$.

• If $0\le x\le\dfrac\pi4$, $$u=\sqrt2\sin\left(x+\frac\pi4\right) \implies x = -\frac\pi4 + \arcsin \frac u{\sqrt2}$$
• If $\dfrac\pi4\le x\le\dfrac\pi2$, $$u=\sqrt2\sin\left(x+\frac\pi4\right) \implies x = \frac{3\pi}4 - \arcsin \frac u{\sqrt2}$$

Notice how $u\in[1,\sqrt2]$ in the first case and $u\in[\sqrt2,1]$ in the second (same interval, but reversed). $u$ is decreasing in the latter, and that's reflected in the sign of the respective $dx$ element. Upon applying the substitution, you would end up with

$$\begin{align*} \int_0^\tfrac\pi2 \frac{dx}{\cos x+\sin x} &= \left\{\int_0^\tfrac\pi4 + \int_\tfrac\pi4^{\tfrac\pi2}\right\} \frac{dx}{\cos x+\sin x} \\ &= \int_1^{\sqrt2} \frac{du}{u\sqrt{2-u^2}} \color{red}{-} \int_{\sqrt2}^1 \frac{du}{u\sqrt{2-u^2}} \\ &= 2 \int_1^{\sqrt2} \frac{du}{u\sqrt{2-u^2}} \end{align*}$$

---

On the other hand, we can avoid all of this confusion by instead replacing $u=x+\dfrac\pi4$ and recalling the primitive of $\csc u$ :

$$\begin{align*} \int_0^\tfrac\pi2 \frac{dx}{\cos x+\sin x} &= \frac1{\sqrt2} \int_0^\tfrac\pi2 \csc\left(x+\frac\pi4\right) \, dx \\ &= \frac1{\sqrt2} \int_\tfrac\pi4^{\tfrac{3\pi}4} \csc u \, du\\ &= -\frac1{\sqrt2} \left(\ln\left|\csc\frac{3\pi}4+\cot\frac{3\pi}4\right| - \ln\left|\csc\frac\pi4+\cot\frac\pi4\right|\right) \\ &= \frac1{\sqrt2} \ln \frac{\sqrt2+1}{\sqrt2-1} \equiv \sqrt2 \operatorname{artanh}\frac1{\sqrt2} \end{align*}$$

Answer 3

As user170231 said, OP’s substitution is NOT injective on $[0,1]$ to guarantee the existence of its inverse. We have to use the other bijective substitutions such as $y=x-\frac \pi2$ on $[0,1] $ whose graph is

$$\begin{aligned} \int_0^{\frac{\pi}{2}} \frac{1}{\cos x+\sin x} d x =&\frac{1}{\sqrt{2}}\int_0^{\frac{\pi}{2}} \frac{d x}{\cos \left(x-\frac{\pi}{4}\right)} \\ = & \sqrt{2} \int_0^{\frac{\pi}{4}} \sec y d y \\ = & \sqrt{2}[\ln |\sec y+\tan y|]_{0}^ \frac{\pi}{4} \\ = & \sqrt{2} \ln (\sqrt{2}+1) \end{aligned} $$

Or we can use $t=\tan \frac x2$ whose graph is

$$ \begin{aligned} I & =\int_0^1 \frac{1}{\frac{1-t^2}{1+t^2}+\frac{2 t}{1+t^2}} \frac{2 d t}{1+t^2} \\ & =2 \int_0^1 \frac{d t}{-t^2+2 t+1} \\ & =-2 \int_0^1 \frac{d t}{(t-1)^2-2} \\ & =-\frac{1}{\sqrt{2}}\left[\ln \left|\frac{t-1-\sqrt{2}}{t-1+\sqrt{2}}\right|\right]_0^1\\&=\sqrt{2} \ln (\sqrt{2}+1) \end{aligned} $$

Answer 4

Another approach for integrals involving quotients of trigonometric functions is to employ the Weierstrass Substitution: $$ t = \tan\left(\frac{x}{2}\right) \longrightarrow dx = \frac{2}{1+t^2}\:dt, \quad \sin\left(x\right) = \frac{2t}{1+t^2},\quad \cos\left(x\right) = \frac{1 - t^2}{1 + t^2} $$ In doing so, you can covert the integrand from a trigonometric expression into an algebraic form: $$ I = \int_0^1 \frac{1}{\frac{1 - t^2}{1 + t^2} + \frac{2t}{1+t^2}} \cdot \frac{2}{t^2+1}\:dt = 2\int_0^1 \frac{1}{1 + 2t -t^2}\:dt = 2\int_0^1 \frac{1}{2 - \left(t - 1\right)^2}\:dt $$ Let $u = t - 1$ and so $du = dt$: \begin{align} I &= \int_{-1}^0 \frac{1}{2 - u^2}\:du = \int_{-1}^0 \frac{1}{\left(\sqrt{2} + u\right)\left(\sqrt{2} - u\right)}\:du = \int_{-1}^0 \frac{1}{2\sqrt{2}}\left[\frac{1}{\sqrt{2} + u} + \frac{1}{\sqrt{2} - u}\right]\:du \\ &=\frac{1}{2\sqrt{2}}\bigg[\ln\left(\sqrt{2} + u\right) - \ln\left(\sqrt{2} - u\right) \bigg]_{-1}^0 = \frac{1}{2\sqrt{2}}\left[ \ln\left(\frac{\sqrt{2} + u}{\sqrt{2} - u}\right)\right]_{-1}^0 = \frac{1}{2\sqrt{2}}\left[\ln\left(\frac{\sqrt{2} +1}{\sqrt{2} - 1}\right)\right] \end{align}