radius = 3
Let $y-y_1 = m(x-x_1)$ be the equation of tangent.
Since, tangent passes through (3,4)
$or,\text{ }y - 4 = m(x - 3)$
$or,\text{ }y - 4 = mx - 3m$
$or,\text{ }mx +y - 3m + 4 = 0$
Thus, center of given circle is $(0,0)$. So, the perpendicular distance from the center to the tangent.
$or,\text{ }p = \big | \frac{ax_1 + by_1+c}{\sqrt{a^2+b^2}}\big |$
$or,\text{ }p = \big | \frac{a.0 + b.0 +4-3m}{\sqrt{{m}^2+1^2}}\big |$
$or,\text{ }p = \big | \frac{4-3m}{\sqrt{{m}^2+1^2}}\big |$
$or,\text{ }p^2 = \frac{(4-3m)^2}{{{m}^2+1^2}}$
As perpendicular distance from tangent to center = radius of circle,
$or,\text{ }9m^2 + 9 = 16 + 9m^2 - 24m$
$or,\text{ }m = \frac{7}{24}$
I wonder why one solution only? and Solve this further
-
1$m=\infty$ is also a solution – David Quinn Apr 07 '24 at 19:12
-
Is there any condition for one tangent line? It may have two tangent intersect with each other at (3, 4) and the point is outside of circle. – Abhishek Kharel Apr 07 '24 at 19:12
-
But when I tried to create tangent equation. I got a problem. – Abhishek Kharel Apr 07 '24 at 19:14
-
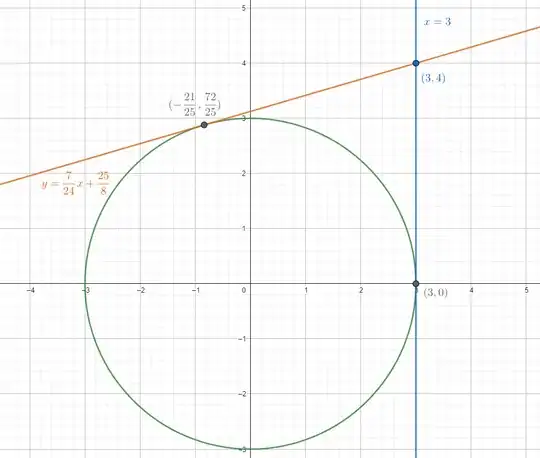
The line $x = 3$ is also tangent to the circle and passes through $(3,4)$, but is not of the form $y - y_1 = m(x-x_1)$. – Ennar Apr 07 '24 at 19:15
-
3Try drawing a picture – David Quinn Apr 07 '24 at 19:16
-
Please help me to solve this further by posting answer. – Abhishek Kharel Apr 07 '24 at 19:21
-
@AbhishekKharel, but Point(3,4) isn't on this circle.. So either the radius isn't 3, or you have a typo in the point coordinates. – Stanislav Bashkyrtsev Apr 07 '24 at 19:26
-
@StanislavBashkyrtsev, no, it's not on the circle and it's not a typo. – Ennar Apr 07 '24 at 19:27
-
2@Ennar, the question states that the tangent needs to go through the point$(3,4)$ on the circle. So it's not just a line that passes through $(3,4)$ and is a tangent to the circle. Or maybe the question is simply phrased ambiguously ¯\(ツ)/¯ – Stanislav Bashkyrtsev Apr 07 '24 at 19:32
-
1@StanislavBashkyrtsev it's poorly worded, but there is nothing mathematically problematic, it is obvious that we are trying to find all lines tangent to the circle $x^2+y^2 = 9$ that go through point $(3,4)$. – Ennar Apr 07 '24 at 19:38
-
2The equation $(y - y_1) = m (x - x_1)$ can represent all the lines in the plane except the "vertical" lines that are parallel to the $y$ axis. The second tangent is one of those lines. That's why you are getting only one value for $m$. – Gribouillis Apr 07 '24 at 19:46
-
"Please help me to solve this further by posting answer." sounds like you just want us to post an answer so you can copy-paste it into your homework. – jjagmath Apr 07 '24 at 20:15
-
$(x^2+y^2-9)(3^2+4^2-9)-(3x+4y-9)^2 = (x - 3)(7 x - 24 y + 75)$ – Jan-Magnus Økland Apr 07 '24 at 20:19
-
No that’s not my homework. I know that m=tan(90)=infinite but why doesn’t it shows in equations. Mind your word @jjagmath. It’s not for homework. I have already solve this just i got one solution. So, I was surprised and i was wondering it. So, I came here in this platform. – Abhishek Kharel Apr 09 '24 at 13:21
4 Answers
Let $(a,b)$ be a point on the circle $x^2+y^2 = 9$. Then the line $a(x-a)+b(y-b) = 0$ is line tangent to the circle that passes through point $(a,b)$. We also want point $(3,4)$ to be on the line $a(x-a)+b(y-b) = 0$ so we get system
\begin{align} a(3-a)+b(4-b) &= 0\\ a^2+b^2 &= 9 \end{align}
If we expand the first equation we get $3a+4b-(a^2+b^2) = 0$ and substituting $a^2+b^2 = 9$, the system becomes
\begin{align} 3a+4b &= 9\\ a^2+b^2 &= 9 \end{align}
From the first equation we get $a = 3-\frac 43 b$, which you can substitute into the second equation and get two solutions $a=3,b=0$ and $a=-\frac{21}{25}, b=\frac{72}{25}$.
Finally, substitute that back into tangent line equation $a(x-a)+b(y-b) = 0$, first solution gives the line $3(x-3) + 0(y-0) = 0$, i.e. $x = 3$ and the second solution gives the line $-\frac{21}{25}(x+\frac{21}{25})+\frac{72}{25}(y-\frac{72}{25}) = 0$, i.e. $y = \frac 7{24}x+\frac{25}8.$
Your approach is correct and gives the tangent line $y = \frac 7{24}x+\frac{25}8$, but not the line $x = 3$. This is because you assumed that tangent line is of the form $y-y_1 = m(x-x_1)$, but $x = 3$ is not of that form, so you only got one line. If you want to finish the exercise your way, you can repeat the process but assume that you have tangent line of the form $m(y-y_1) = x-x_1$. You should get $m = 0$.
- 24,364
I am actually busy right now but I will expand my answer later of you wish.
Use the $SS_1=T^2$ method and then factorise the resultant expression. You'll get both the tangents.
In this answer $S$ denotes the equation of circle, $S_1$ denotes the numerical value we get after putting the coordinate given in the equation of the circle and $T$ denotes the equation of chord of contact.
Proof click here
- 10,058
-
Would be great if you could expand this answer at some point, very curious :) – Stanislav Bashkyrtsev Apr 08 '24 at 09:55
-
@StanislavBashkyrtsev this is what my comment to the question does – Jan-Magnus Økland Apr 08 '24 at 13:45
The fact that the $m^2$ term cancels from your equation indicates that $m=\infty$ is a valid solution. This value corresponds to the vertical tangent.
- 35,087
HINT
Calculus-based answer. I would start with noticing that \begin{align*} x^{2} + y^{2} = 9 \Rightarrow 2x + 2yy' = 0 \Rightarrow y' = -\frac{x}{y} \end{align*}
Let $(x_{0},y_{0})\in \partial B_{3}(0)$. If $y_{0} = 0$, then $(x_{0},y_{0}) = (3,0)$ is a solution.
If $y_{0}\neq 0$, one gets the following system of equations to solve: \begin{align*} \begin{cases} x^{2}_{0} + y^{2}_{0} = 9\\\\ y_{0} - 4 = -\dfrac{x_{0}}{y_{0}}(x_{0} - 3) \end{cases} & \Longleftrightarrow \begin{cases} x^{2}_{0} + y^{2}_{0} = 9\\\\ x^{2}_{0} + y^{2}_{0} - 3x_{0} - 4y_{0} = 0 \end{cases} \Longleftrightarrow \begin{cases} x^{2}_{0} + y^{2}_{0} = 9\\\\ 3x_{0} + 4y_{0} = 9 \end{cases} \end{align*}
Can you take it from here?
- 18,937