I used your DESMOS Output to make this Image :
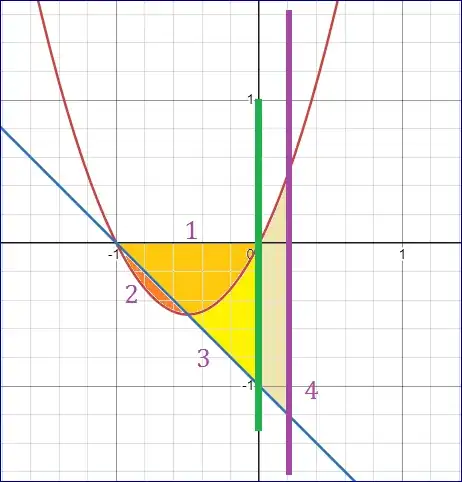
I have shaded & marked 4 general regions.
In general , (1) is the area between 2 functions & the $X$ Axis.
It could be Positive (above the Axis) or negative (below the Axis) like in this Case.
Then (2) is the area between 2 functions , where we have to Identify "Exactly" 2 Points of Intersection.
When there are more than 2 Intersections , it will be ill-defined & we have to give additional Criterion.
Moving to (3) , it is the area between some $X$ Co-ordinate (here it is $x=0$ ) & nearest Point of Intersection , which we have to Identify.
When there are Intersections on both sides of that $x$ Co-ordinate , it will be ill-defined & we have to give additional Criterion.
Lastly , (4) is the area between 2 functions between 2 $x$ Co-ordinates.
There are certain complications when there are Intersections between these limits , which I will not get into at the moment.
Coming to OP Case , we should know what the Exact Wording was to know what was intended.
Assuming certain things , we can say that Area (3) was to be calculated.
ADDENDUM :
OP is wondering whether it is (3) or (3)+(2) or (3)+(2)+(1).
Well , it can not be (3)+(2) or (3)+(2)+(1) because :
(A) In general , there might be multiple Intersections when $x$ is negative , like with 2 functions involving $sin$ terms. We can not go indefinitely backwards looking for all Intersections to include in the area.
(B) At every Intersection , Area Polarity changes & accounting for that is not standard. Certain Situations require that we add up the magnitudes. Certain Situation require that we add & subtract accordingly.
(C) Such Complications are not handled in Intro-Level text-books , hence we are left with only (3) to Evaluate.
