Hamiltonian Circuit Counting and Classification Problem

Question

Consider an undirected complete graph $G_n$ with $n$ vertices, where if the numerical labels of each vertex are consecutive, then the edge between them is $1$, and the edge between the numerical labels on first and last vertices is also $1$. The edge between any other pair of vertices is $n$.

Based on this property, consider a Hamiltonian circuit vertex arrangement $(a_1, a_2, \ldots, a_n)$, which is composed of edges of $n$ and $1$, so its is $k \cdot n + (n - k)$, where $k$ represents the number of edges of $n$ in the arrangement.

For example, the arrangement $(1,2,3,4)$ corresponds to $k=0$, and the arrangement $(1,3,2,4)$ corresponds to $k=2$, because the edges $(1,3)$ and $(2,4)$ are not numerical consecutive, so there are $2$ edges of $n$.

The question is:

(1) Given the number $k$ of edges of $n$, how many Hamiltonian circuits have a of $k \cdot n + (n - k)$? In other words, the question can be transformed into:

How many Hamiltonian circuits contain $k$ edges of $n$?

What is known so far by my intuition($n\geq 7$):

• When $k=0$, there is $1$ circuit.
• When $k=1$, there is no circuit.
• When $k=2$, there are $\frac{n(n-3)}{2}$ circuits.
• When $k=n-2$, the number of circuits does not exceed $\frac{20}{6!} \cdot n \cdot (n-2)!$.

However, for other cases, there is currently no method of estimation.

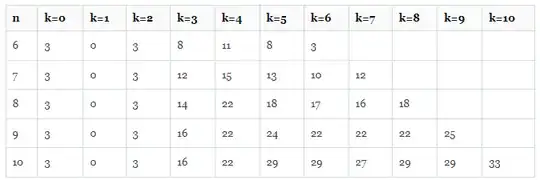
Here is my numerical experiment on $n=5$ to $n=11$

(2) For a given permutation of $V(G_n)$ given by: $$H=(\pi_1,\pi_2,...,\pi_{i-1},\pi_{i},\pi_{i+1},...,\pi_{j-1},\pi_{j},\pi_{j+1},...,\pi_n),$$ a 2-opt swap operation, $\eta_{i,j}(H)$, transforms $H$ into another permutation, specifically: $$H'=\eta_{i,j}(H)=(\pi_1,\pi_2,...,\pi_{i-1},\pi_{j},\pi_{j-1},...,\pi_{i+1},\pi_{i},\pi_{j+1},...,\pi_n),$$ In $H'$, the vertices from the $1$st to the $i-1$th in $H$ are copied with the same order to $H'$, while the vertices from the $i$th to the $j$th in $H$ are reversed and copied into $H'$. Finally, the vertices from the $j+1$th to the $n$th in $H$ are maintained in the same order and copied to $H'$.

In the complete graph $G_n$, we divide the set $\mathcal{H}$ of all Hamiltonian cycles into layers based on the number of edges of length $n$ they contain: $$L_i = \{H \in \mathcal{H} : w(H) = in + n - i, i = 0, \dots, n\}.$$ Then we define: $$\sigma_{k \to k+l}(H) = \#\{i \in \{1, \dots, n\}, j \in \{i+1, \dots, n\} : \eta_{i,j}(H) \in L_{k+l}, H \in L_{k}\},$$ which means the total number of possible operations for edges that can transition a Hamiltonian cycle $H$ in layer $L_k$ to layer $L_{k+l}$ through a 2-opt operation.

For example, if $H = (3,6,1,2,4,5)$, then: $$\sigma_{3 \to 3}(H) = \#\{(1,2),(1,3),(1,5),(1,6),(2,6),(3,6),(4,6)\} = 7,$$ because:

$\eta_{1,2}(H) = (6, 3, 1, 2, 4, 5) \in L_3$

$\eta_{1,3}(H) = (1, 6, 3, 2, 4, 5) \in L_3$

$\eta_{1,5}(H) = (4, 2, 1, 6, 3, 5) \in L_3$

$\eta_{1,6}(H) = (5, 4, 2, 1, 6, 3) \in L_3$

$\eta_{2,6}(H) = (3, 5, 4, 2, 1, 6) \in L_3$

$\eta_{3,6}(H) = (3, 6, 5, 4, 2, 1) \in L_3$

$\eta_{4,6}(H) = (3, 6, 1, 5, 4, 2) \in L_3$

We define $\xi_{k \to k+l} = \{\sigma_{k \to k+l}(H) : H \in L_k\}$ as the set of all possible numbers of operations for elements in layer $L_k$ to transition to layer $L_{k+l}$.

Question is, given $n, k, l$, determine the bounds for $|\xi_{k \to k+l}|$.

For this question, there is currently no clear solution strategy.

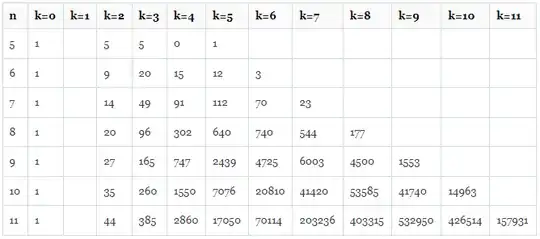
Here is my numerical experiment on $n=5$ to $n=11$ and $l=0$

the meaning of number in the cell=$\max\{\sigma_{k\to k+l}(H):H\in L_k\}$

Answer 1

I can answer Question 1 exactly. I have no ideas about Question 2.

For each $r\in \{1,\dots,n-1\}$, define $$ a_r= \sum_{t=1}^r \frac nt \binom{r-1}{t-1}\binom{n-r-1}{t-1}\cdot 2^{t-1}\cdot (n-r-1)!\tag1 $$ Furthermore, let $a_0=(n-1)!/2$, and let $a_n=1$.

For all $n\ge 3$ and $k\in \{0,1\dots,n\}$, the number of Hamiltonian cycles which contain $k$ edges of length $n$, and $n-k$ edges of length $1$, is $$ \boxed{\sum_{r=n-k}^n(-1)^{r-n+k}\binom{r}{n-k}a_r.}\tag2 $$ This formula reproduces your table exactly. Try it online!

---

To prove this, we apply the generalized principle of inclusion exclusion. Let $U$ be any set, and let $E_1,\dots,E_n$ be subsets of $U$. We think of the subsets $E_i$ as properties; if $u\in E_i$, then $u$ has the $i^\text{th}$ property. The question is, for each $p\in \{0,1,\dots,n\}$, how many elements of $U$ have exactly $p$ properties?

To answer this, for each $r\in \{0,1,\dots,n\}$, let $a_r$ be the number of ways to choose a subset of $r$ properties, and then choose an element of $U$ with all of those properties. The generalized PIE says that $$ \text{# elements with exactly $p$ properties}=\sum_{r=p}^{n}(-1)^{r-p}\binom rp a_r\tag3 $$ For more discussion of this result, see Generalised inclusion-exclusion principle.

To apply this to your problem, let $U$ be the set of Hamiltonian cycles. As long as $n\ge 3$, then $|U|=(n-1)!/2$. For each $i\in \{1,\dots,n\}$, let $E_i$ be the set of Hamiltonian cycles in $U$ which use the edge of length $1$ joining $i$ to $i+1$.

We want to find the number of Hamiltonian cycles which use exactly $n-k$ edges of length $1$. To apply the generalized PIE, we let $a_r$ be the number of ways to select $r$ edges of length $1$ and then choose a Hamiltonian cycle which uses all of the selected edges.

I will now prove that $a_r$ is indeed given by the formula in $(1)$. Define a run in a Hamiltonian cycle to be a segment of vertices which only use length one edges. I will specifically count the number of ways to choose $r$ edges of length $1$ which form $t$ runs. Let $x_1,x_2,\dots,x_t$ be the lengths of the runs. Between each pair of runs, there is an interval of edges of length $n$; let $y_1,\dots,y_t$ be the lengths of these intervals, where $y_i$ is the interval between $x_i$ and $x_{i+1}$. The numbers $x_1,\dots,x_t,y_1,\dots,y_t$ satisfy $$ \begin{align} x_1+\dots+x_t&=r,\\ y_1+\dots+y_t&=n-r,\\ x_i\ge 1,\;\;y_i&\ge 1\quad \forall i \end{align} $$ Using stars and bars, the number of ways to choose integers satsifying the above is $$\binom{r-1}{t-1}\cdot \binom{n-r-1}{t-1}$$ The factor of $\binom{r-1}{t-1}$ chooses the $x_i$'s, while the factor of $\binom{n-r-1}{t-1}$ chooses the $y_i$'s. However, we have just specificed the lengths of these runs, and the spaces between; we still need to choose their location on the circle. It turns out that the factor which accounts for this is $n/t$. If you choose one of the $t$ intervals as a reference point, then there are $n$ places you can choose to place that interval, which forces the entire placement. However, this gives a special role to that interval; this introduces overcounting, which is fixed by dividing by $t$.

We are almost done explaining the formula for $(1)$. Now that we have grouped the numbers in $\{1,\dots,n\}$ into several runs, we need to actually arrange these in a Hamitonian cycle. We started with $n$ numbers, and then we joined $r$ pairs of numbers together using edges of length $1$, leaving $n-r$ blocks. These can be arranged in a circle in $(n-r-1)!$ ways (for circular permutations of $m$ objects, the number is $(m-1)!$). Finally, we need to choose the orientation of each of the $t$ runs, because they can each go backwards or forwards. This would give a factor of $2^t$, but because the Hamiltonian cycle is unchanged when you reverse its order, we only really have $t-1$ degrees of freedom, so there are $2^{t-1}$ ways to choose the orientation.

This explains $(1)$. Finally, applying the generalized PIE exactly results in $(2)$.

Answer 2

A Hamiltonian cycle using $k$ "crossing edges" ("crossing edges" are edges of weight $n$) will be formed by a $k$-partition of the "unit weight cycle" (where the subsets are made of consecutive vertices) and a Hamiltonian cycle visiting every subset in one or the other direction.

The number of $k$-partition of an $n$-vertex cycle is $\frac{n}{n-k}\binom{n-k}{k}$ (it can be found by stars and bars). The number of Hamiltonian cycles visiting the subsets is $(k-1)!$ In the Hamiltonian cycle between subsets, when leaving a subset, we have at most two choices to enter the next subset, one for each extremity. There are two cases where it does not hold: when the next subset is of size $1$ (so both choices are the same) and when the next subset is adjacent to the last visited vertex of the current subset (one of the choices will not be a crossing edge). But in the worst case, we have two choices to be made $k$ times. Thus we can bound the number of arrangements by: $$\frac{n}{n-k}\binom{n-k}{k}2^k(k-1)!$$ I guess this bound should be somewhat good when $k$ is neither small (many adjacent subsets will be visited consecutively) nor close to $n$ (many subsets will have size $1$). A lower bound will be: $$\frac{n}{n-k}\binom{n-k}{k}(k-1)!$$