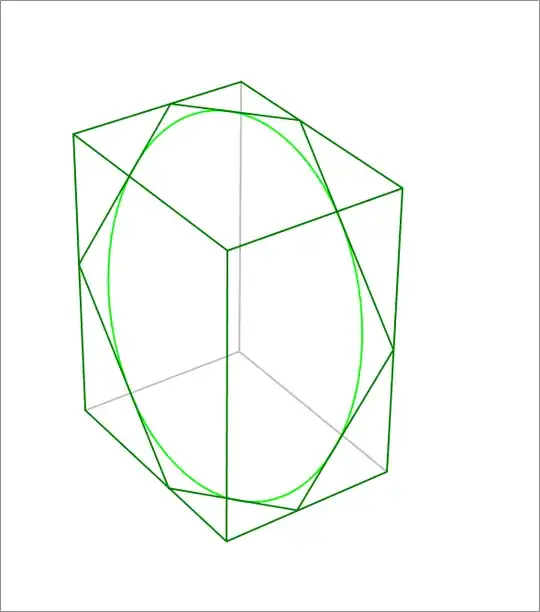
Suppose you're given a cuboid centered at the origin, and with its edges parallel to the coordinate axes. Suppose its measure is known to be $2 a \times 2 b \times 2 c $ along the $x, y, z$ directions, respectively.
Further suppose you have a plane with unit normal $n$, that cuts through the faces of the cuboid. Assume that this cutting plane cuts through all six faces of the cuboid.
Question: Now, I'd like to find the parametric equation of the ellipse that lies in the cutting plane, centered at the origin, that is tangent to all the faces of the cuboid.
My thoughts:
The intersection of the cutting plane with the faces of the cuboid results in an irregular hexagon, but one that has parallel opposite sides. The ellipse is obviously centered at the origin, so it is determined by $3$ parameters. Using tangency to three consecutive sides of the hexagon of intersection, these parameters can be determined.