0

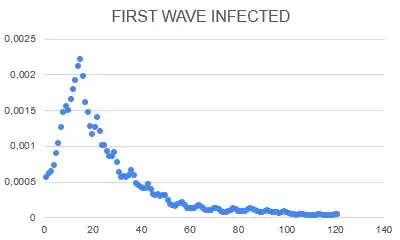
I'm trying to model the COVID-19 pandemic in Madrid during the first wave, to model the data I'm using the SIR model. The SIR model stands for suceptible, infected and recovered. It is a compartmental model meaning that it puts each person in one of the comparments and it models how each individual moves between the compartments.

The model is based on a system of ODE's with two parameters "a" and "b". The system is the following:

$\frac{dS}{dt}=-bsi$ (1)

$\frac{dI}{dt}=bsi-ai$ (2)

$\frac{dR}{dt}=ai$ (3)

I have the data for the active cases each day (Infected compartment) and i'm trying to numerically obtain the value for the parameter "b" (I already know "a"). Perhaps the least squares method could work to estimate the values but I'm not sure how I could apply it here.

enter image description here

The main method i've used (but has not worked) is solving the ODE implicitly. By diving equation (2) by equation (1) you end up with a solution for i(t) in terms of S(t).

$i=i(t)=\frac{a}{b}ln(s(t))-s(t)-i(0)-\frac{a}{b}ln(s(0))+s(0)$

From here you can express the value of "b" in terms of s(t) and i(t)

$b=\frac{aln(\frac{s(t)}{s(0)})}{i(t)+s(t)+i(0)-s(0)}$

And since I have the data for s(t) and i(t) I calculated the value of "b" for all the different days in the first wave and I calculated the mean of these values, however the model doesn't corectly fit the data with the mean parameter that I obtained.

Matin Gomez-Pablos
  • 31
  • It would be good that you detail what you tried. Also, Cross Validated may be a better fit for your question. – mathcounterexamples.net Mar 30 '24 at 17:16
  • Least squares is 100% the way to go here. Write a function that takes in $b$ and outputs the squared error of the solution compared to the data then feed it to your favorite optimization routine. – whpowell96 Mar 30 '24 at 17:50
  • This initial data does not reflect the spread of a new illness but the artificially organized spread of a new (likely fraudulent) test. As the number of tests was restricted, the search proceeded after some heuristic patterns, and the reproduction of these patterns in the test results was uncritically taken as proof that these patterns are natural and show the spread of something new. Circular reasoning. The first arc most likely reflects the ramp-up in test production, not some infection spread. Another problem is the size of the initially susceptible population. – Lutz Lehmann Mar 30 '24 at 18:27
  • The data you show, what variables do they belong to? – Cesareo Mar 30 '24 at 22:06
  • 1
    Presumably the data corresponds to the infected proportion, $i(t)$. – whpowell96 Mar 31 '24 at 02:10

0 Answers0