$$\begin{gathered}
\frac{{{x^3} + 4}}{{{{\left( {x + 1} \right)}^3}}} = c \hfill \\
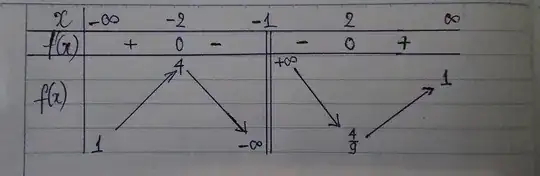
* {\text{Let}}:f\left( x \right) = \frac{{{x^3} + 4}}{{{{\left( {x + 1} \right)}^3}}}{\text{ so the domain is }}\mathbb{R}\backslash\left\{ { - 1} \right\} \hfill \\
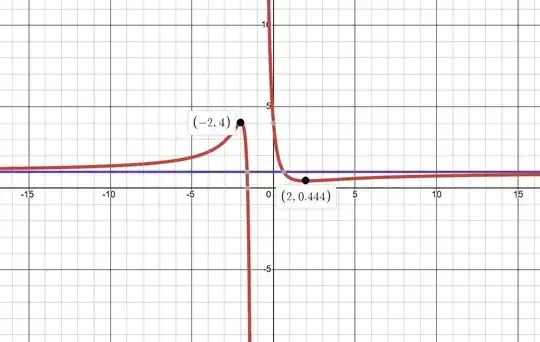
f'\left( x \right) = \frac{{3\left( {{x^2} - 4} \right)}}{{{{\left( {x + 1} \right)}^4}}} \Rightarrow f'\left( x \right) = 0 \Leftrightarrow x = \pm 2 \Rightarrow f\left( 2 \right) = \frac{4}{9},f\left( { - 2} \right) = 4 \hfill \\
f'\left( x \right) \geqslant 0 \Leftrightarrow \left[ \begin{gathered}
x \geqslant 2 \hfill \\
x \leqslant - 2 \hfill \\
\end{gathered} \right.,f'\left( x \right) < 0 \Leftrightarrow x \in \left( { - 2, - 1} \right) \cup \left( { - 1,2} \right) \hfill \\
{\text{Also}}:\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = - \infty ,\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \infty ,\mathop {\lim }\limits_{x \to \infty } = 1,\mathop {\lim }\limits_{x \to - \infty } = 1 \hfill \\
{\text{See the variation table, then the line }}y = c{\text{ intersect at 2 points where }}c = \frac{4}{9},1,4 \hfill \\
\end{gathered}$$