1. Question Summary (for Easier Reference)
Solve for the indefinite integral:
$$\int \frac{dx}{2x^4 + 3x^2 + 5} \tag{Eq. 1}$$
2. Solution Steps
First find the roots of
$2x^4 + 3x^2 + 5=0$ as follows:
$$2x^4 + 3x^2 + 5=0\underset{implies}{\implies} \\
x^4 + \frac{3}{2}x^2 + \frac{5}{2}=0\underset{implies}{\implies} \\
\left(x^2+\frac{3}{4}\right)^2=\left(-\frac{5}{2}\right)
+\left(\frac{3}{4}\right)^2
= \left(-\frac{40}{16}\right)+\left(\frac{9}{16}\right)\\
\underset{implies}{\implies}
\left(x^2+\frac{3}{4}\right)^2
=\left(-\frac{31}{16}\right) \\
\underset{implies}{\implies}
(x^2)_\pm
=\frac{3}{4}\pm \sqrt{\left(-\frac{31}{16}\right)}=
\frac{3}{4} \pm i*\sqrt{\left(\frac{31}{16}\right)} $$
$$\tag{Eqs. 2}$$
From Equation 1, and the roots found in Equation 3, now:
$$\int{\frac{dx}{2x^4+3x^2+5}}=
\int{\frac{1}{2}\frac{dx}{x^4+\frac{3}{2}x^2+\frac{5}{2}}}=\\
=\int{\frac{k_1}{x^2+c_1}}+\int{\frac{k_2}{x^2+c_2}}= \\
=\int{\frac{k_1}{x^2+(-(x^2)_+)}}+\int{\frac{k_2}{x^2+(-(x^2)_-)}}= \\
=\int{\frac{1}{2}
\frac{\displaystyle 1}
{\displaystyle \left(x^2-(x^2)_+\right)
\left(x^2-(x^2)_-\right)
}
}$$
$$
\tag{Eqs. 3}$$
Following the Stack Exchange Mathematics Question
"Prove that if $f=\frac{1}{(x-a_1)*(x-a_2)...}$, then $f=\frac{k_1}{x-a_1}+\frac{k_2}{x-a_2}+...$ where $k_1=\frac{1}{(a_1-a_2) ... }$ distinct $a_i$" and Answer, from Equations 3, $k_1$ and $k_2$ can be found as follows. Multiply Equation 4 below on the left and the right by $x^2+(-(x^2)_+)$ to yield Equation 5.
$$
\int{\frac{k_1}{x^2+(-(x^2)_+)}}+\int{\frac{k_2}{x^2+(-(x^2)_-)}}
=\int{\frac{1}{2}
\frac{\displaystyle 1}
{\displaystyle \left(x^2-(x^2)_+\right)
\left(x^2-(x^2)_-\right)
}
}
$$
$$\tag{Eq. 4}$$
$$
\int{k_1}+\int{
\frac{(k_2)({x^2+(-(x^2)_+)})}
{x^2+(-(x^2)_-)}
}
=\int{\frac{1}{2}
\frac{\displaystyle 1}
{\displaystyle
\left(x^2-(x^2)_-\right)
}
}
$$
$$\tag{Eq. 5}$$
And set $x^2=(x^2)_+$ to yield the solution for $k_1$ as follows in Equation 6a and consider the symmetry of $k_1$ and $k_2$ to arrive at the solution for $k_2$ in Equation 6b as follows:
$$
\int{k_1}
=\int{\frac{1}{2}
\frac{\displaystyle 1}
{\displaystyle (x^2)_+ - (x^2)_-}
}
\text{ , } $$
$$\tag{Eq. 6a}$$
$$
\int{k_2}
=\int{\frac{1}{2}
\frac{\displaystyle 1}
{\displaystyle (x^2)_- - (x^2)_+}
}
=-\int{k_1}
$$
$$\tag{Eqs. 6b}$$
$$\tag{Eqs. 6}$$
Now consider $\int{\frac{1}{u^2+1} du}$. If
$u=\tan{\theta}=
\frac{\sin \theta}{\cos \theta}$ then
$\frac{du}{d \theta} = \frac{d}{d\theta} \frac{\sin \theta}{\cos \theta}
=\frac{1}{(\cos \theta)^2}
\left((\cos \theta)^2 + (\sin \theta)^2 \right)
=(\sec \theta)^2$. So $d u=(\sec \theta)^2 d \theta$. And also, there is the trignometric identity that $1+(\tan \theta)^2 =
\frac{(\cos \theta)^2+(\sin \theta)^2}
{(\cos \theta)^2}=\frac{1}{(\cos \theta)^2}
=(\sec \theta)^2$.
$$\text{So }
\int{\frac{1}{u^2+1} du}=\int{d \theta}=\theta + C \tag{Eqs. 7}$$
So basically by applying these constant definitions, and trigonometric identity for the integral $u=\frac{x}{a}$, $\int{\frac{1}{1+a^2}}$ can be solved using the following route from the on-line integral calculator:
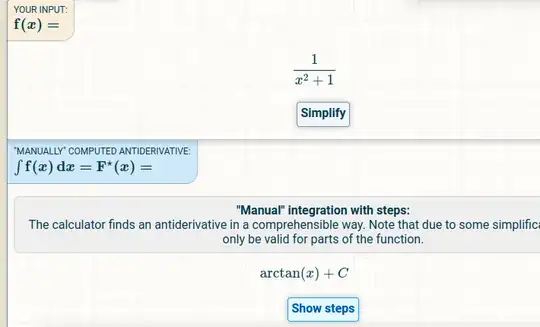
Together with the "Inverse tangent of a complex variable" definition, these steps allow a solution to be completed.
I am hoping to update this article with more step-by-step specifics, but the information already here should lead to an adequate solution.
3. Solution Implementation From the Given Steps
From:
$$f(x)=\int \frac{dx}{2x^4 + 3x^2 + 5} \tag{Eq. 1}$$
Solve:
$$(x^2_\pm)^2+\frac{3}{2}(x^2_\pm)+\frac{5}{2}=0
\underset{implies}\implies\left((x^2_\pm) + \frac{3}{4}\right)^2
=\frac{9}{16}-\frac{5}{2}=\frac{9-40}{16}=-\frac{31}{16}
\tag{Eq. 2.1}$$
Equation 2.1 implies that:
$$
(x^2_\pm)=-\frac{3}{4} \pm i \frac{\sqrt{31}}{4}
\text{ where }i=\sqrt{-1} \\
(x^2_+)=-\frac{3}{4} + i \frac{\sqrt{31}}{4} \text{, and }
(x^2_-)=-\frac{3}{4} - i \frac{\sqrt{31}}{4}
\tag{Eqs. 2.2}$$
Then
$$f'(x) = \frac1{2}
\frac1{\displaystyle x^2+\frac{3}{4}- i \frac{\sqrt{31}}{4}}*
\frac1{\displaystyle x^2+\frac{3}{4}+ i \frac{\sqrt{31}}{4}}\tag{Eq. 2.3}$$
Now, $\int \frac1{1+x^2} dx = \arctan{x}+C$. So consider the solution of the integral $\int\frac1{a^2+x^2} dx$. Let $u=\frac{x}{a}$ then $du=\frac{dx}{a}$. So
$$\int\frac1{a^2+x^2} dx=
\int\frac1{a^2}\frac1{1+\left(\frac{x}{a}\right)^2} a*\frac{dx}{a}
=\frac1{a}\int \frac1{1+\left(\frac{x}{a}\right)^2}*\frac{dx}{a}
\\ \underset{implies}\implies
\int\frac1{a^2+x^2} dx=\frac1{a}\arctan{\frac{x}{a}}+C
\tag{Eqs. 2.4}$$
Now consider what is to be done with the product
$\frac1{x^2-x^2_+}*\frac1{x^2-x^2_-}*$. It is simplified according to this link that can be summarized as (for distinct $a$ and $b$):
$$
\frac1{u+a}*\frac1{u+b}=\frac1{a-b}*\left(\frac1{u+b}-\frac1{u+a}\right)
\tag{Eq. 2.5}$$
This can be proven by multiplying the left and right of Equation 2.5 by $\left(u+a\right)*\left(u+b\right)$ yielding
$1=\frac1{a-b}\left((u+a)-(u+b)\right)=1$ as was to be shown. So Equation 2.3 can be rearranged as:
$$
f'(x) = \frac1{2}
\frac1{\displaystyle x^2+\frac{3}{4}- i \frac{\sqrt{31}}{4}}*
\frac1{\displaystyle x^2+\frac{3}{4}+ i \frac{\sqrt{31}}{4}}=\\
f'(x)=\frac{i}{\sqrt{31}}*\left(
\frac1{\displaystyle x^2+\frac{3}{4}+ i \frac{\sqrt{31}}{4}}-
\frac1{\displaystyle x^2+\frac{3}{4}- i \frac{\sqrt{31}}{4}}
\right)
\tag{Eqs. 2.6}$$
From this Stack Exchange Math reference "Inverse tangent of a complex variable" it follows:
$$\tan^{-1}(z) = \frac{i}{2}\ln\left(\frac{i + z}{i - z}\right)
\underset{implies}\implies \\
\underset{implies}\implies \frac1{a_\pm}\arctan\left(\frac{z}{a_\pm}\right)=
\frac{i}{2}*\frac1{a_\pm}*\ln\left(\frac{i*a_\pm + z}{i*a_\pm - z}\right)
\tag{Eqs. 2.7}$$
Thus, with $(a^2)_+=\frac{3}{4}+ i \frac{\sqrt{31}}{4}$ and
$(a^2)_-=\frac{3}{4} - i \frac{\sqrt{31}}{4}$.
And $(a)_+=\sqrt{\frac{3}{4}+ i \frac{\sqrt{31}}{4}}$, and
$(a)_-=\sqrt{\frac{3}{4} - i \frac{\sqrt{31}}{4}}$. Then:
$$
f(x)=\int{f'(x)}dx$$
$$
\boxed{
f(x)
=-\frac1{2*\sqrt{31}}*\left(
\frac1{a_+}*\ln\left(\frac{i*a_+ + x}{i*a_+ - x}\right)
-\frac1{a_-}*\ln\left(\frac{i*a_- + x}{i*a_- - x}\right)
\right)+C}$$
$$\textit{where C is the integration constant of the indefinite integral.}
$$ $$\tag{Eqs. 2.8}$$
Further simplification of Equation 2.8 is more than likely to result in a clearer result. However, the current steps have already gone a lot further towards the end result and should be helpful for those proceeding this far at least. I hope to update this section further, time permitting.
