Symmetries in regular "floral" circle patterns (seed of life etc.)

Question

Consider $n$ equally sized circles $c_i$ in the plane with their centers $x_i$ in the vertices $v_i$ of a regular $n$-gon and all meeting in the center of that $n$-gon.

Examples:

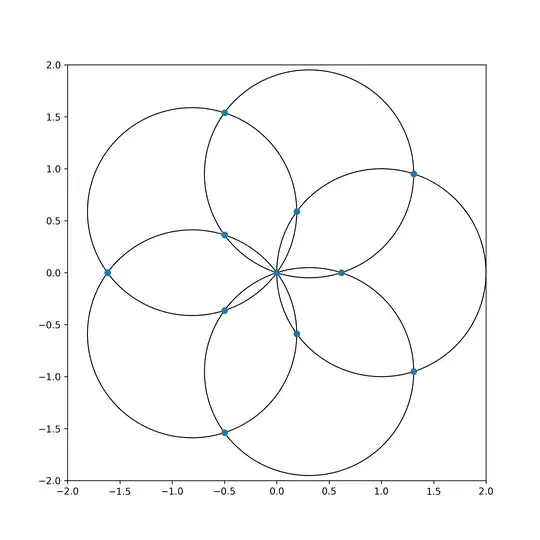
• Fig. 1: circle pattern for $n=5$:

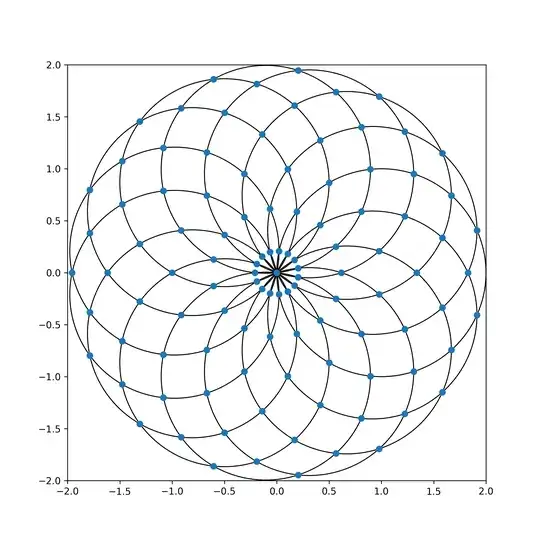
• Fig 2: circle pattern for $n=15$:

For each pattern, the circles partition the plane into many cells with cell corners defined by circle intersection points (marked blue) and circle arcs as cell border lines. Most cells are bounded by 4 intersection points with exceptions for the innermost and outermost cells.

Observation: all those arcs have the same length, except for the innermost (having half of that length) and the outermost triangular cells (having one double-length arc).

It clearly has to do with all those symmetries, but I failed to find a proper argument for a proof as the cells themselves are not all congruent.

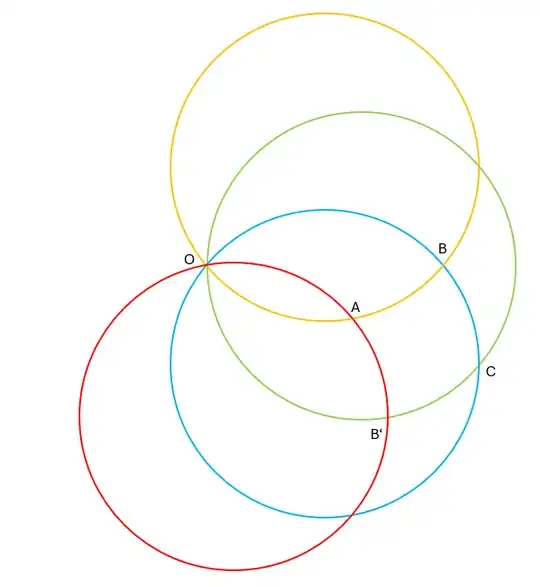
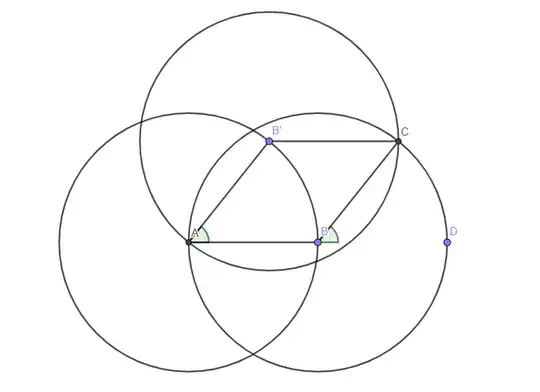
• Fig 3: shows a detail for $n=9$ with 4 consecutive circles all having point $O$ in common and rotated by the same angle. Due to symmetry $|AB|=|AB'|$ and $|BC|=|B'C|$. But, why is $|AB|=|BC|$?

Any clue is highly appreciated.

Answer 1

We fix a circle (here, the one with center $B$), and we rotate the circle by an angle (to get the circle centered in $B'$. By construction, we easily see that $ABCD$ is a diamond and that the intersection $C$ is placed at the same angle that the circle was rotated.

Because rotations of the other circles are regular, the intersections are regularly spaced on the circle.

The center $A$ is never counted as such an intersection, so the two "one half" arcs are just one full arc. We can see the point $D$ as the intersection of the circle with itself, so where we have a double-length arc, we can see it as just two arcs.