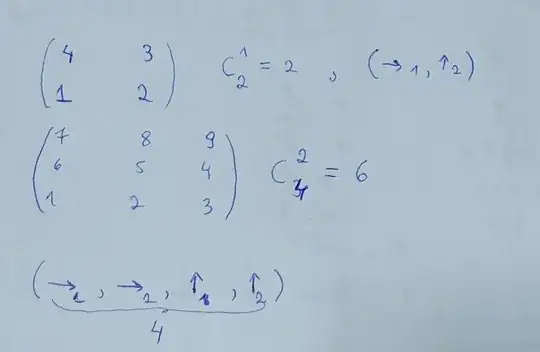I have the matrix in the image for a reference.
I can't understand why using combinations work on finding all the minimal paths. (In the image, I go from bottom-left to top-right).
For the first matrix we use Combinations of 2 elements taken once, but who those 2 elements are?? (Are they the right-arrows and up-arrows meaning).
Same for the 4 by 4 matrix. Do the elements I'm arranging look like those I put below the matrix? (right1, right2, up1,up2).
Example of a correct minimal path:1 2 5 8 9 or 1 2 5 4 9 Wrong would be: 1 2 5 6 7 8 9 or 1 2 3 2 5 8 9
I'm not sure it made sense, if not, please just explain however you can...