I need to show that the following tricky integral: $$\int_0^\pi{12\cos x\ \mathrm{sech}\left(\frac {\pi}2\tan\frac x2\right)}\mathrm{d}x$$ is equal to exactly $\pi^2$. I have no idea how to start. I tried the substitution $u=\tan\frac x2$ and ended up with:
$$\int_0^\infty24\ \mathrm{sech}\frac{\pi u}{2}\frac{1-u^2}{(1+u^2)^2}\mathrm{d}u$$
I might have to use residue theorem or Fourier transformation here, but I'm lost. Thank you!
Continue with \begin{align} &\int_0^\infty \operatorname{sech}\frac{\pi x}{2}\frac{1-x^2}{(1+x^2)^2}dx\\ =& \int_0^\infty \operatorname{sech}\frac{\pi x}{2}\bigg(\int_0^\infty e^{-y} y \cos(x y) dy\bigg) dx\\ =& \int_0^\infty e^{-y}y \int_0^\infty \frac{\cos (xy)}{\cosh\frac{\pi x}2}dx \ dy =\int_0^\infty \frac{ e^{- y}y} {\cosh y} \overset{t=e^{-2y}}{dy}\\ =& - \frac12\int_0^1 \frac{\ln t}{1+t}dt\overset{ibp}= \frac12\int_0^1 \frac{\ln (1+t)}{t}dt=\frac{\pi^2}{24}\\ \end{align} where $\int_0^\infty \frac{\cos (xy)}{\cosh\frac{\pi x}2}dx=\text{sech}\ y$ and $ \int_0^1 \frac{\ln (1+t)}{t}dt =\frac{\pi^2}{12}$.
We will prove
$$ \int_{0}^{\pi}\cos\left(x\right)\operatorname{sech}\left(\frac{\pi}{2}\tan\frac{x}{2}\right)\,dx=\frac{\pi^{2}}{12}\,. $$
PROOF
Let $\mathcal{I}$ be the integral in question. We use the mapping $x \mapsto 2\arctan x$ to get
$$ \begin{align} \mathcal{I} &\stackrel{\Delta}{=} \int_{0}^{\pi}\cos\left(x\right)\operatorname{sech}\left(\frac{\pi}{2}\tan\frac{x}{2}\right)\,dx \\ &=2\int_{0}^{\infty}\operatorname{sech}\left(\frac{\pi x}{2}\right)\frac{1-x^{2}}{\left(1+x^{2}\right)^{2}}\,dx \\ &= \int_{\mathbb{R}}\operatorname{sech}\left(\frac{\pi x}{2}\right)\frac{1-x^{2}}{\left(1+x^{2}\right)^{2}}\,dx \\ &= 2\Re\int_{\mathbb{R}}\frac{e^{\pi x /2}}{\left(e^{\pi x}+1\right)\left(1+ix\right)^{2}}\,dx\,. \end{align} $$
Next, we define a holomorphic function $f: \mathbb{C}\setminus\left\{(2k+1)i \in \mathbb{C} : k \in \mathbb{Z}\right\} \longrightarrow \mathbb{C}$ where $z \mapsto \frac{e^{\pi z/2}}{\left(e^{\pi z}+1\right)\left(1+iz\right)^{2}}$. Every element of the set $\left\{(2k+1)i \in \mathbb{C} : k \in \mathbb{Z}\right\}$ are simple poles, except the third order pole $i$ when $k=0$. Also, we construct a simple, counterclockwise, and closed contour in the shape of an isosceles triangle $\mathcal{T}$ with vertices at $(-2N,0)$, $(2N,0)$, and $(0,2N)$. We express this triangle as $[-2N,2N] \cup T_1 \cup T_2$ where
$$ \begin{align} T_1 &\stackrel{\Delta}{=} \left\{2Ni+it-t \in \mathbb{C}: t \in [-2N,0]\right\} \\ T_2 &\stackrel{\Delta}{=} \left\{2Ni-it-t \in \mathbb{C}: t \in [0,2N]\right\}\,. \\ \end{align} $$
The set of poles that $\mathcal{T}$ encloses is
$$ P_n \stackrel{\Delta}{=} \left\{(2n+1)i \in \mathbb{C} : 0 \leq n \leq N-1\right\}\,, $$
where $n$ and $N$ are non-negative integers such that $n < N$.
Here is a visual of the contour with the domain coloring and shading of $f$.
$$ \text{Counterclockwise Triangle Contour $\mathcal{T}$ With Domain Coloring} $$
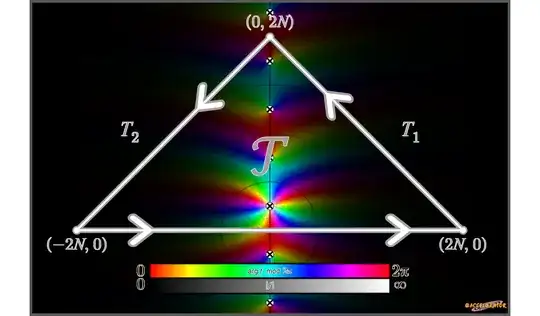
See this Desmos link for an automatic animation of the contour I made. As $N$ grows, none of the odd integer poles touch it because we judiciously constructed $\mathcal{T}$ where its top vertex lies between two poles.
With this contour, we construct a sequence of contour integrals $\oint_{\mathcal{T}}f$ such that $\oint_{\mathcal{T}}f$ converges as $N \to \infty$. We express the contour integral as
$$ \oint_{\mathcal{T}}f = \int_{-2N}^{2N}f+\int_{T_{1}}^{ }f+\int_{T_{2}}^{ }f\,. $$
Taking $N \to \infty$ on both sides, we get
$$ \lim_{N \to \infty}\oint_{\mathcal{T}}f = \int_{\mathbb{R}}f+\lim_{N \to \infty}\int_{T_{1}}^{ }f+\lim_{N \to \infty}\int_{T_{2}}^{ }f\,. $$
We will prove that the integral over $T_1$ vanishes as $N$ goes to $\infty$ using the Estimation Lemma and the Squeeze Theorem for sequences.
We obtain the length of $T_1$ from the Distance Formula:
$$ \sqrt{\left(2N-0\right)^{2}+\left(0-2N\right)^{2}}=2\sqrt{2}N\,. $$
In addition, we obtain the upper bound of $|f|$:
$$ \begin{align} |f| &= \left|\frac{e^{\frac{\pi z}{2}}}{\left(e^{\pi z}+1\right)\left(1+iz\right)^{2}}\right| \\ &\leq \frac{\left|e^{\frac{\pi z}{2}}\right|}{\left|1-\left|e^{\pi z}\right|\right|\cdot\left|1-\left|z\right|\right|^{2}} \\ &\overset{z \in T_1}{=} \frac{\left|e^{\frac{\pi}{2}\left(2Ni+it-t\right)}\right|}{\left|1-\left|e^{\pi\left(2Ni+it-t\right)}\right|\right|\cdot\left|1-\left|2Ni+it-t\right|\right|^{2}} \\ &= \frac{1}{e^{\frac{\pi t}{2}}\left(e^{-\pi t}-1\right)\left(\sqrt{\left(2N+t\right)^{2}+t^{2}}-2\right)^{2}}\,. \\ \end{align} $$
We employ the Estimation Lemma and obtain the inequality
$$ \left|\int_{T_{1}}^{ }f\right|\le\frac{2\sqrt{2}N}{e^{\frac{\pi t}{2}}\left(e^{-\pi t}-1\right)\left(\sqrt{\left(2N+t\right)^{2}+t^{2}}-2\right)^{2}}\,. $$
Taking the limit as $N \to \infty$ of the upper bound, we get
$$ \lim_{N \to \infty}\frac{2\sqrt{2}N}{e^{\frac{\pi t}{2}}\left(e^{-\pi t}-1\right)\left(\sqrt{\left(2N+t\right)^{2}+t^{2}}-2\right)^{2}} = 0 $$
because the numerator grows asymptotically slower than the denominator.
The Squeeze Theorem concludes that
$$ \lim_{N \to \infty} \left|\int_{T_{1}}^{ }f\right| = 0 $$
which means
$$ \lim_{N \to \infty} \int_{T_{1}}^{ }f = 0\,. $$
By a similar process, we could also evaluate the contour integral over $T_2$, which is
$$\lim_{N \to \infty}\int_{T_{2}}^{ }f = 0\,.$$
Going back to $\oint_{\mathcal{T}}f$, we use the famous Cauchy's Residue Theorem and apply $N \to \infty$ to get
$$ \begin{align} \oint_{\mathcal{T}}f &= 2\pi i\sum_{n \in P_n}\mathop{\mathrm{Res}}_{z=(2n+1)i} f \\ \implies \lim_{N \to \infty}\oint_{\mathcal{T}}f &= 2\pi i\sum_{n=0}^{\infty}\mathop{\mathrm{Res}}_{z=(2n+1)i} f \\ &= \underbrace{2\pi i\mathop{\mathrm{Res}}_{z=i} f}_{\text{third-order pole}} + \underbrace{2\pi i\sum_{n=1}^{\infty}\mathop{\mathrm{Res}}_{z=(2n+1)i} f}_{\text{simple poles}}\,. \\ \end{align} $$
First, we calculate the residue of $f(z)dz$ at the third-order pole. Note that $f(z) = -\frac{1}{2\left(z-i\right)^{2}}\operatorname{sech}\left(\frac{\pi z}{2}\right)$. With some algebra, we expand $\operatorname{sech}\left(\frac{\pi z}{2}\right)$ as the asymptotic
$$ -\frac{2i}{\pi\left(z-i\right)}+\frac{i\pi}{12}\left(z-i\right)-\frac{7\pi^{3}i}{2880}\left(z-i\right)^{3}+\mathcal{O}\left(\left(z-i\right)^{5}\right) $$
which is the Laurent series centered at $z=i$. Multiplying $-\frac{1}{2\left(z-i\right)^{2}}$ by each term of the series yields the coefficient of $\frac{1}{z-i}$ as
$$ \mathop{\mathrm{Res}}_{z=i} f = -\frac{i\pi}{24}\,. $$
Second, we solve for the infinite sum of residues at the simple poles. Using the piecewise equality
$$ e^{k\pi i} = \begin{cases} 1 & k \equiv 0 \pmod{2} \\ -1 & k \equiv 1 \pmod{2}\,, \tag{1}\\ \end{cases} $$
we do the following tedious calculations:
$$ \begin{align} \mathop{\mathrm{Res}}_{z=(2n+1)i} f &= \lim_{z \to (2n+1)i}\frac{e^{\frac{\pi z}{2}}}{\frac{d}{dz}\left(\left(e^{\pi z}+1\right)\left(1+iz\right)^{2}\right)} \\ &= \lim_{z \to (2n+1)i}\frac{e^{\frac{\pi z}{2}}}{\left(1+iz\right)\left(2i+e^{\pi z}\left(\pi+2i+\pi iz\right)\right)} \\ &= \frac{e^{\frac{\pi}{2}\left(2n+1\right)i}}{\left(1+i\left(2n+1\right)i\right)\left(2i+e^{\pi\left(2n+1\right)i}\left(\pi+2i+\pi i\left(2n+1\right)i\right)\right)} \\ &\overset{(1)}{=} -\frac{i\left(-1\right)^{n}}{4\pi n^{2}}\,. \\ \end{align} $$
Putting all the residues together, we have
$$ \begin{align} \lim_{N \to \infty}\oint_{\mathcal{T}}f &= 2\pi i\left(-\frac{i\pi}{24}\right)-2\pi i\sum_{n=1}^{\infty}\frac{i\left(-1\right)^{n}}{4\pi n^{2}} \\ &= \frac{\pi^{2}}{12}+\frac{1}{2}\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n}}{n^{2}} \\ &= \frac{\pi^{2}}{12}+\frac{1}{2}\left(-\frac{1}{1^{2}}+\frac{1}{2^{2}}-\frac{1}{3^{2}}+...\right) \\ &= \frac{\pi^{2}}{12}+\frac{1}{2}\left(-\frac{1}{1^{2}}-\frac{1}{2^{2}}-\frac{1}{3^{2}}-...+2\left(\frac{1}{2^{2}}+\frac{1}{4^{2}}+\frac{1}{6^{2}}+...\right)\right) \\ &= \frac{\pi^{2}}{12}+\frac{1}{2}\left(-\sum_{m=1}^{\infty}\frac{1}{m^{2}}+2\cdot\frac{1}{2^{2}}\sum_{l=1}^{\infty}\frac{1}{l^{2}}\right) \\ &= \frac{\pi^{2}}{12}+\frac{1}{2}\left(-\frac{\pi^{2}}{6}+\frac{1}{2}\cdot\frac{\pi^{2}}{6}\right) \\ &= \frac{\pi^{2}}{24}\,. \\ \end{align} $$
Gathering all our results together, we finally recover the integral we want:
$$ \begin{align} &\require{cancel}{\frac{\pi^{2}}{24} = \int_{\mathbb{R}}\frac{e^{\pi x /2}}{\left(e^{\pi x}+1\right)\left(1+ix\right)^{2}}\,dx + \cancelto{0}{\lim_{N \to \infty}\int_{T_{1}}f}+\cancelto{0}{\lim_{N \to \infty}\int_{T_{2}}f}} \\ \implies 2\Re&\frac{\pi^{2}}{24} = 2\Re\int_{\mathbb{R}}\frac{e^{\pi x /2}}{\left(e^{\pi x}+1\right)\left(1+ix\right)^{2}}\,dx\,. \end{align} $$
We finally conclude with
$$ \bbox[15px,#eefef8,border:5px outset #4f9a8f]{\int_{0}^{\pi}\cos\left(x\right)\operatorname{sech}\left(\frac{\pi}{2}\tan\frac{x}{2}\right)\,dx=\frac{\pi^{2}}{12}} $$
and the proof is done! $\blacksquare$
I might upload my second solution depending on how I feel.
COMMENT.-By definitions $$I=\int_0^\pi{12\cos(x)\ \mathrm{sech}\left(\frac 12\pi\tan\left(\frac x2\right)\right)}\mathrm{d}x$$ $$I=\int_0^\pi6\cos(x)( e^A-e^{-A}) dx\text { where } A={\frac 12\pi\tan(\frac x2)}$$ or$$I=\int_0^\pi6\cos(x)(e^B-e^{-B})dx\text { where } B=\frac12\pi\sqrt{\frac{1-\cos(x)}{1+\cos(x)}}$$ where, obviously $$A=B=\tan(\frac x2)=\sqrt{\frac{1-\cos(x)}{1+\cos(x)}}$$ What results with changes of possible variables is always non-elementary. My opinion is that there is no clever trick possible as you believe.
