Minimum $k$ for which every positive integer of the interval $(kn,(k+1)n)$ is composite

Question

I am looking for references containing results on the minimum $k$ for which every positive integer of the interval $(kn,(k+1)n)$ is composite.

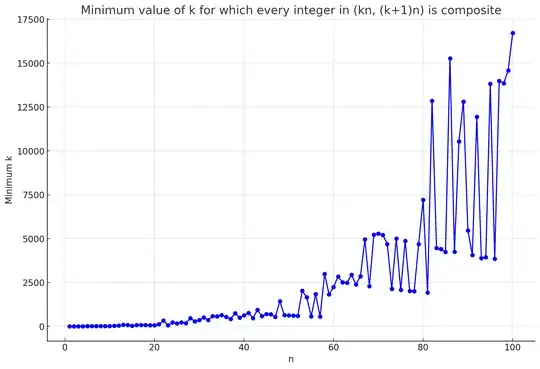
If we denote as $k(n)$ this minimum $k$ for some $n$, $k$ is indeed always equal or greater than $n+2$, and grows exponentially as $n$ grows. I attach the graph of $k(n)$ for $n\leq 100$.

The exponential growth could be reasonable, and suggests that some exponential lower bound for $k(n)$ could indeed be established for all $n>N_0$.

What I do not find "so reasonable" is the great variations that appear between $k(n)$ and $k(n+1)$.

So,

My questions:

• Is there any result concerning lower bounds of $k(n)$? I will appreciate the references of any paper addressing $k(n)$.

• Why do we have this great variation between $k(n)$ and $k(n+1)$ for so many $n$?

Thanks for your time!

EDIT

After reviewing the partial answer provided by @Eric, it surprises me that, looking at the exponential growth showed in the graph, it has not even been established a lower bound of $k(n)$ equal or greater than $n+2$. Why is such a result so difficult?

After having a closer look at the minimum intervals at each $k(n)$, it seems that a necessary condition for having that every positive integer of the interval $(kn,(k+1)n)$ is composite is that at least one of those composites is not divisible by prime numbers less or equal than $n$. Is that so? I can provide examples for $k(n\leq 3)$:

$k(2)=4$

We need the first composite number of the form $2x+1$. It is straightforward that this number is $3^2=9$, and thus $k(2)=4$.

$k(3)=8$

We need the first consecutive composite numbers of the form $3x+1$ and $3x+2$. It is clear that $2$ divides one of them, and $3$ does not divide any of them; therefore, it is straightforward that the minimum odd number of the wanted pair is $5^2=25$, and thus $k(3)=8$.

Despite these easy cases, a general proof seems difficult. It would need to be shown (through a process similar, or different, that the one I have showed for $n\leq 3$) that for consecutive integers $nx+1, nx+2,..., nx+(n-1)$ it is impossible that all of them are divisible by prime numbers less than $n$ if $x\leq n+2$.

Answer 1

Partial answer:

Another way to consider $k(n)$ is by looping through prime gaps that are at least $n$ and finding one which contains two consecutive multiples of $n$. Denote the location of the first prime gap of at least length $n$ as $m_n$. Since a gap of at least $n$ is necessary and a gap of length $2n$ always gives such consecutive numbers, this gives that $$m_n/n \leq k(n)\leq m_{2n}/n$$

Large jumps can occur because the start of $m_n$ or any similar gaps might not line up perfectly with multiples of $n$, so you can bounce in between those two bounds.

I’d recommend plotting $n\times k(n)$. In particular, you should see some interesting constant lines across your graph. This is already apparent on your graph, where it looks like there are some long straightish horizontal lines in your graph, from 65 to 82 and 70 to 98 which probably correspond to a few large prime gaps around 15k and 400k that are causing these. For example, the first length 96 gap starts at 360653. The table with the maximal prime gaps can be found here and is instructive: https://en.m.wikipedia.org/wiki/Prime_gap

Bounds on prime gaps therefore will give bounds on $k(n)$.

As an extreme example, $(n+1)!+2$ through $(n+1)!+n+1$ are composite, so $m_n\leq (n+1)!$, so $k(n)$ is $O((2n)!)$.

On the other side of the spectrum, we need something which gives an upper bound on gaps. Betrand’s Postulate is too weak, but Dusart’s strengthening says there’s a prime between $c$ and $x(1+1/(2\ln(x)^2)$ for $x\geq 3275$, so $m_n>2 n \ln(n)^2$, so $k(n)>2 \ln(n)^2$ for large enough $n$. The largest gap below 3275 is 34 at 1327, so it’s at least true for $n>34$. This is still pretty weak, and better estimates will improve bounds. The best conjectured bound I can find is there being a prime between $x$ and $x+2\sqrt{x}$ which would suggest a lower bound of $n/4$, so (unless I’ve made a mistake somewhere), showing exponential lower bounds seems impossible.