Background
I've recently been formulating a game that incorporates elements from Egyptian fractions, magic squares, and tilings. It is a single-player game in which the objective is to tessellate a square with sides of length $1$ with tiles that have the surface area of unit fractions. A sum of distinct unit fractions is called an Egyptian fraction.
Let's call an 'Egyptian unity sum set' (EUSS) a set of distinct positive integers $\{ a_{1}, a_{2}, \dots , a_{n} \}$ of size $n$ such that their Egyptian fraction sum to $1$. So we have $$ \frac{1}{c_{1}} + \frac{1}{c_{2}} + \dots + \frac{1}{c_{n}} = 1. $$
For instance, $\{2,3,6\}$ is an EUSS for $n=3$.
Moreover, we say that an Egyptian unity sum set is composite if $c_{1}, \dots , c_{n}$ are all composite numbers. An example of a composite EUSS is $\{4, 6, 8, 9, 10, 12, 15, 18, 24\}$. In this case, $n=9$. There are no such sets for $n<9$. But for every $n \geq 9$, there is at least one. More information can be found in this question.
The Game
We will be tiling unit squares with rectangles that each have the surface area corresponding to the reciprocal of the elements of the composite Egyptian sum sets. The sides of the rectangles are also of unit fraction length. The lengths must correspond to a factorization of the multiplicative inverse of the numbers in the composite Egyptian sum sets. That is, for a composite EUSS $\{c_{1}, \dots , c_{n}\}$ we have:
\begin{align*}1 &= \ \ \ \ \ \ \ \ \ \frac{1}{c_{1}} \ \ \ \ \ \ \ \ + \ \ \ \ \ \ \ \ \frac{1}{c_{2}} \ \ \ \ \ \ \ \ + \ \ \ \ \dots \ \ \ + \frac{1}{c_{n}} \newline &= \left(\frac{1}{a_{1}} \times \frac{1}{b_{1}} \right) + \left(\frac{1}{a_{2}} \times \frac{1}{b_{2}} \right) + \dots + \left(\frac{1}{a_{n}} \times \frac{1}{b_{n}} \right)\end{align*} The equation below describes some composite EUSS factorization. The $n$ rectangles thus have dimensions $\left(\frac{1}{a_{1}} \times \frac{1}{b_{1}}\right), \dots , \left(\frac{1}{a_{n}} \times \frac{1}{b_{n}} \right)$. Here, we require that $a_{i} \neq 1$ and $a_{i} \neq c_{i}$ for all $i$. The same holds for all $b_{i}$. If there are multiple possible factorizations of a number (like $12 = 3 \times 4 = 2 \times 6 $), then one may use tiles with unit fraction lenghts that correspond to the factorization of your own choosing.
Finally, we require that all the rectangles are used exactly once to tile the unit square. So no double tiles or missing tiles are allowed. A tiling with all such rectangles used only once is called a magic Egyptian tiling (MET).
Non-examples
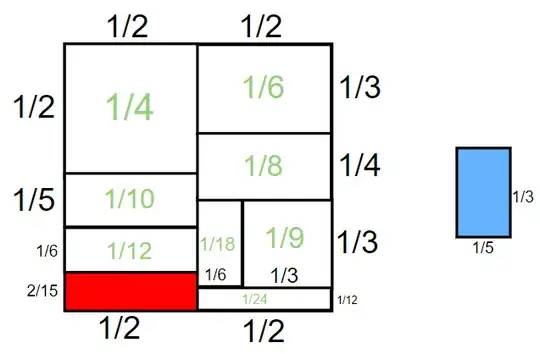
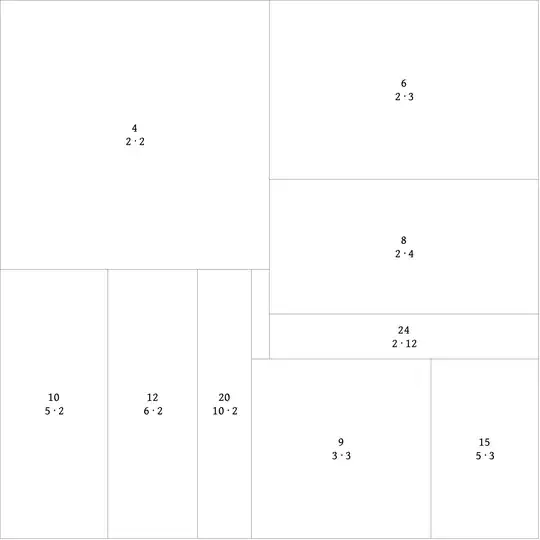
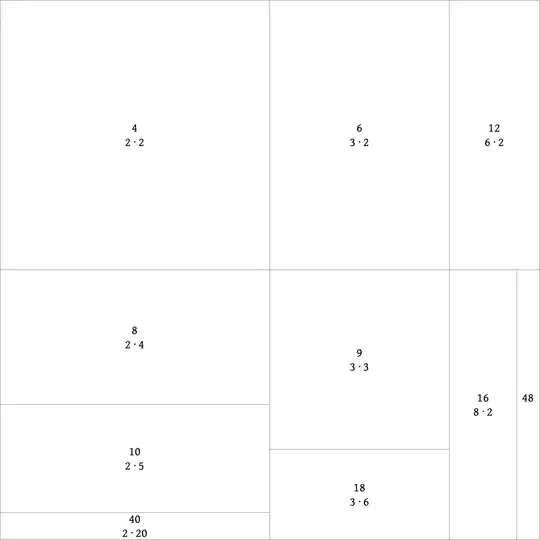
I've been trying to find METs for the EUSS described above: $\{4, 6, 8, 9, 10, 12, 15, 18, 24\}$. Unfortunately, I haven't been successful yet. Here are two failed attempts at tilings. The size of the rectangles is annotated in green.
(1)
We see that it is almost an MET, but not quite. The remaining blue tile of size $\frac{1}{15}$ does not fit in the remaining red space of the unit square. Moreover, the lengths of the sides of the red rectangle are not both unit fractions.
Here, we employed the factorization \begin{align*} 1 &= \ \ \ \ \ \frac{1}{4} \ \ \ \ \ + \ \ \ \ \ \frac{1}{6} \ \ \ \ \ + \ \ \ \ \ \ \frac{1}{8} \ \ \ \ \ + \ \ \ \ \ \ \frac{1}{9} \ \ \ \ \ + \ \ \ \ \frac{1}{10} \ \ \ \ \ + \ \ \ \ \frac{1}{12} \ \ \ \ \ + \ \ \ \ \frac{1}{15} \ \ \ \ \ + \ \ \ \ \frac{1}{18} \ \ \ \ \ + \ \ \ \ \frac{1}{24} \newline &= \left( \frac{1}{2} \times \frac{1}{2} \right) + \left( \frac{1}{2} \times \frac{1}{3} \right) + \left( \frac{1}{2} \times \frac{1}{4} \right) + \left( \frac{1}{3} \times \frac{1}{3} \right) + \left( \frac{1}{2} \times \frac{1}{5} \right) + \left( \frac{1}{2} \times \frac{1}{6} \right) + \left( \frac{1}{3} \times \frac{1}{5} \right) + \left(\frac{1}{3} \times \frac{1}{6} \right) + \left(\frac{1}{2} \times \frac{1}{12} \right). \end{align*}
We call this factorization $(3)$.
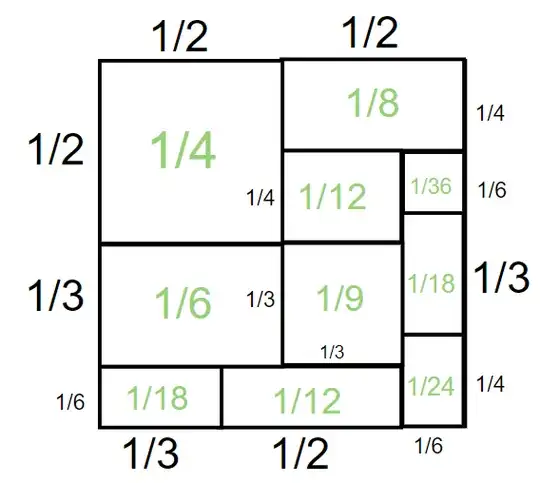
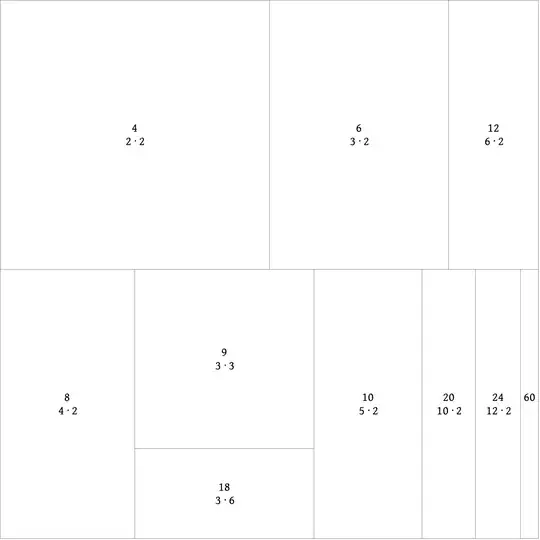
We now move to the second non-example:
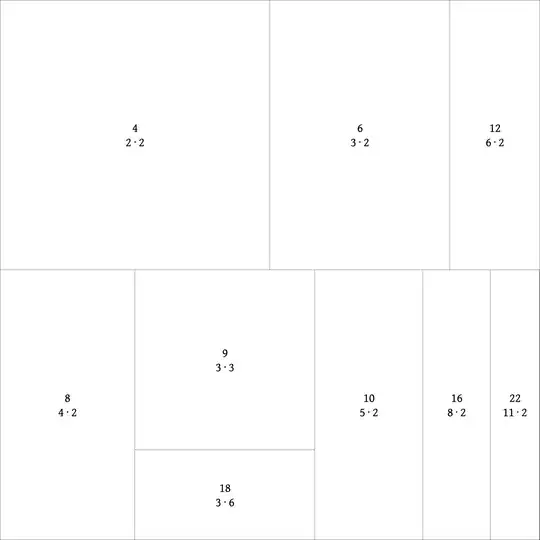
(2)
(Please ignore the unevenness of the square - this is due to my poor drawing skills.)
In this case, all rectangles do tile the unit square. However, there's trouble in paradise: some of the tiles are used twice. The tiles of size $\frac{1}{12}$ and $\frac{1}{18}$ are both employed twice. Moreover, the tiles of size $\frac{1}{10}$ and $\frac{1}{15}$ are missing. This is not allowed.
Questions
- Is there an MET for the EUSS with the factorization described in $(3)$ ?
- Does an MET exist for every composite EUSS factorization?
- If not, does an MET exist for every composite EUSS?
- If not, does an MET exist for all $n \geq 9$ ?