Find surface which generated by revolving a line in $\mathbb{R}^3$

Question

Problem :

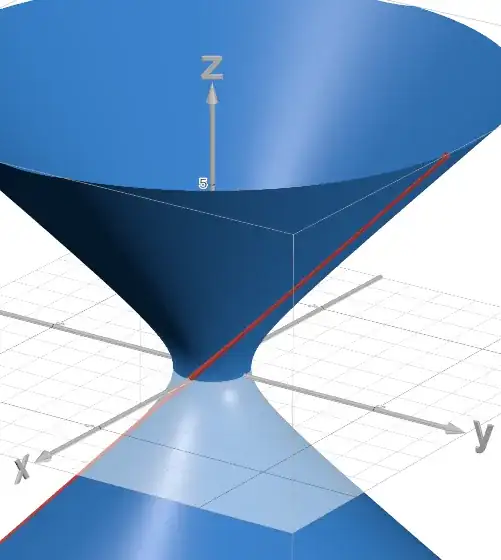
Let $l$ be a line which passes two points : $(1,0,0), (1,1,1)$.

And $S $ be a surface which generated by revolving line $l$ around $z$-axis.

Find a volume enclosed by surface $S$ and two planes : $z=0, z=1$.

---

My Attempt

Parametric equation of $l$ can be obtained easily : $$l(t) = (1,t,t)$$

And, distance $d(t)$ between $l$ and $z$-axis is same with distance between $(0,0, t), (1,t,t)$ : $$d(t) = \sqrt{1+t^2}$$

Since $l(0)=(1,0,0), l(1)=(1,1,1)$, volume $V$ what we want is : $$\begin{align} V &= \pi\int_0^1 d(t)^2 dt \\ &= \pi\int_0^1 (1+t^2)dt \\ &= \frac{4}{3}\pi\end{align}$$

---

Here are my main questions :

1. Is this method legit? If not, I'd like to know what the problem is. If yes, is this method can be used anytime? (For problems which request volume enclosed by surface which generated revolving line or curve and planes.)

2. Can I find equation of $S$ explicitly to evaluate $V$ with triple integral?

Answer 1

Your approach is correct. As regards the second question, the surface S is a one-sheeted hyperboloid which is an example of ruled surface. Indeed, by rotating each point $(1,t,t)$ of the line, individually, we find the disjoint circles $$x^2+y^2=1^2+t^2,\quad z=t, \quad t\in\mathbb{R}.$$ After eliminating the parameter $t$, we obtain the equation $$x^2+y^2=z^2+1.$$

Therefore $V$ is the volume of the solid $$D=\{(x,y,z): x^2+y^2\leq z^2+1, z\in [0,1]\}$$ and we find $$V=\int_{z=0}^1\int_{\rho=0}^{\sqrt{z^2+1}}\int_{\theta=0}^{2\pi} \rho d\theta d\rho dz=\pi\int_{z=0}^1(z^2+1)\,dz=\frac{4}{3}\pi.$$