Is there any way to solve this equation algebraically and give an exact form of the solution: $x^x = (x-1)^{x+1}$? WolframAlpha only finds the approximate solution 4.14.
-
https://math.stackexchange.com/questions/3463603/solve-for-x-in-ax-xb?noredirect=1 maybe helps – Khosrotash Feb 29 '24 at 21:11
-
1See https://oeis.org/A100086. – A rural reader Feb 29 '24 at 21:38
-
This is the Foias constant – Тyma Gaidash Feb 29 '24 at 22:27
1 Answers
Consider the function
$$f(x) = \frac{(x-1)^{x+1}}{x^x}, \quad x > 1$$
and its logarithm
$$g(x) = \log f(x) = (x+1) \log (x-1) - x \log x, \quad x > 1.$$
The original equality is satisfied whenever $g = 0$. A plot of $g$ is shown as follows:
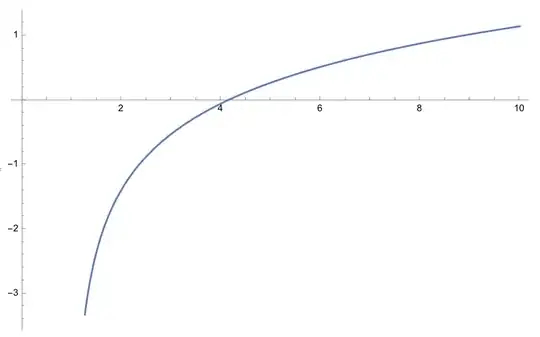 We can compute successive iterates of the Newton's method recursion of $g$ with an initial guess of $x_0 = 4$:
We can compute successive iterates of the Newton's method recursion of $g$ with an initial guess of $x_0 = 4$:
$$x_{n+1} = \frac{2x_n - (x_n - 1) \log (x_n - 1)}{2 + (x_n - 1)\log(1 - 1/x_n)}$$
gives $$\begin{array}{c|c} n & x_n \\ 0 & 4.00000000000000 \\ 1 & 4.13751482760659 \\ 2 & 4.14103935294361 \\ 3 & 4.14104152540996 \\ 4 & 4.14104152541079 \\ 5 & 4.14104152541079 \end{array}$$
When $x < 1$, we run into problems with defining a real-valued function for $(x-1)^{x+1}$, which is why the domain is restricted.
- 143,828