I want to find a way to solve $x^9=3^x$ analytically, for two roots. one of them can be found below $$x^9=3^x\\(x^9)^{\dfrac {1}{9x}}=(3^x)^{\dfrac {1}{9x}}\\x^ { \ \frac 1x}=3^{ \ \frac 19}\\x^ { \ \frac 1x}=(3)^{ \ \frac 3{27}}\\x^ { \ \frac 1x}=(3^3)^{ \ \frac 1{27}}\\
x^ { \ \frac 1x}=(27)^{ \ \frac 1{27}}\\\to x=27$$ but there is a second root if we take a log of both sides and graph them
$$x^9=3^x \to \log x^9 =\log 3^x \to 9\log x=x\log 3$$ 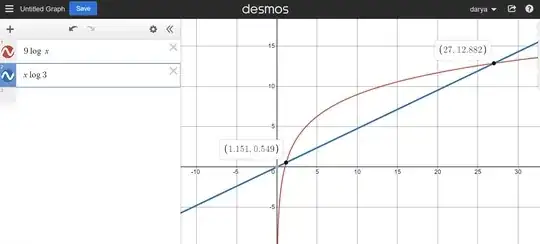
With respect to the picture, there must be $x=1.151$ as another solution, but how can we find it? (without using numerical or graphical methods)
I do appreciate any hint. Thanks