If $x+y=2$ is a tangent to the ellipse with foci $(2, 3)$ and $(3, 5)$, what is the square of the reciprocal of its eccentricity?

Question

If $x+y=2$ is a tangent to the ellipse with foci $(2, 3)$ and $(3, 5)$, what is the square of the reciprocal of its eccentricity?

This could be done by the property, The product of perpendiculars drawn from focus to the tangent is equal to $b^2$. But I couldn't figure out where is error in my approach.

Answer 1

The center of the ellipse is the midpoint between focii, $M=\frac{(2,3)+(3,5)}2=(\frac52,4)$ and the unit vectors of axes are $v_1=(\tfrac1{\sqrt5},\tfrac2{\sqrt{5}})$ and $v_2=(-\tfrac2{\sqrt5},\frac1{\sqrt{5}})$. The ellipse equation is given by $$(x,y)=M+a\cos\theta v_1+b\sin\theta v_2.$$ So the given ellipse is $$\frac{(x+2y-\frac{21}2)^2}{a^2}+\frac{(y-2x+1)^2}{b^2}=5.\tag1$$ The distance between focii is $\sqrt{(3-2)^2+(5-3)^2}=2c=\sqrt5$. Therefore, $$|a^2-b^2|=c^2=\frac54.\tag2$$ On the other hand, if we put the tangent line $y=2-x$ in $(1)$ and equate the discriminant of the resulting quadratic polynomial to zero, after a tedious calculation, we find $$45a^2+4b^2=405.\tag3$$ From $(2)$ and $(3)$, major axis half length is $\frac{\sqrt{41}}2$ and hence, $e=\frac c{\sqrt{41}/2}=\frac{\sqrt5}{\sqrt{41}}$ and $\frac1{e^2}=\frac{41}5.$

Answer 2

The equation of tangent used is wrong. Your formula only works when the centre of the ellipse is at the origin and the axis of ellipse is parallel to x and y axis.

In this case we use a modified version of the same as pointed out by Jan-Magnus Økland in the comments. The centre of this ellipse is ($2.5,4$) and axis of this ellipse are $-2x+y+1=0$ and $x+2y-\frac{21}2=0$

Therefore, in this case we use

$$\frac{-2x+y+1}{\sqrt5}=m\frac{x+2y-\frac{21}2}{\sqrt5}\pm\sqrt{a^2m^2+b^2}$$

Note: I thank @Jan-Magnus Økland for pointing out a major blunder in my answer.

Answer 3

The reciprocal of the square of the eccentricity is $\frac{41}5,$ as you can read off the equations in the two focus/directrix forms below.

One way to get the third listed equation is to start with $$\sqrt{(x-2)^2+(y-3)^2}+\sqrt{(x-3)^2+(y-5)^2}=2a$$ only to square a bit, then to dualize and substitute $(-\frac12,-\frac12)$ (corresponding point in the dual plane of the line $-\frac{x}2-\frac{y}2+1=0$) into giving the equation $128a^2(4a^2-41)(4a^2-5)=0,$ where the other positive solution gives $-4(y-2x+1)^2=0,$ which technically also is a conic section tangent to $x+y+2=0$ going through the foci, but degenerate, so not having the two points as foci. Interestingly this is for $a^2=c^2$ and $b^2=0.$

The fourth listed equation is a version of the standard form, where the semi-axes lengths can be read off. They come out at $\approx 3.2$ and $3.$

$$41((x-2)^2+(y-3)^2-\frac1{\frac{41}5}\frac{(x+2y+10)^2}5)=\\41((x-3)^2+(y-5)^2-\frac1{\frac{41}5}\frac{(x+2y-31)^2}5)=\\ 40x^2 - 4xy + 37y^2 - 184x - 286y +433 =\\ 369(\frac{\frac{(x+2y-\frac{21}2)^2}5}{(\frac{\sqrt{41}}2)^2}+\frac{\frac{(-2x+y+1)^2}5}{3^2}-1)=0.$$

Checking in M2

I=ideal(40*x^2-4*x*y+37*y^2-184*x-286*y+433,x+y-2)
primaryDecomposition I -- ideal(x+y-2,(3*y-5)^2)

$x+y-2=0$ really is a tangent for this ellipse with $(x,y)=(\frac13,\frac53)$ as the tangent point.

Answer 4

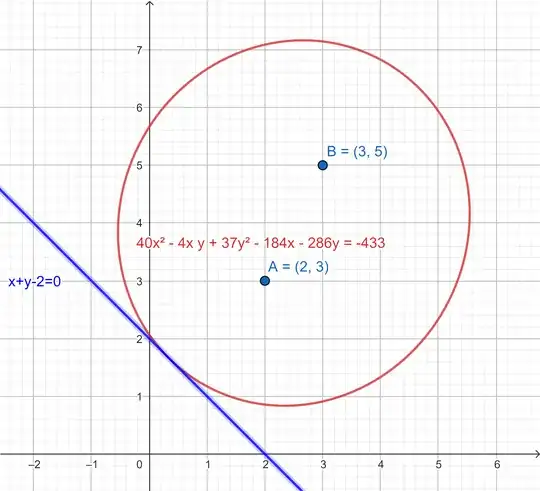
Let $F_1 = (2,3), F_2 = (3,5)$. At a point $P = (x,y)$ on the line $x+y=2$, the normal to this line bisects the angle between $PF_1$ and $PF_2$, that is, the line acts as a mirror for the ray coming out of $F_1$ towards the line, and reflects it at $P$ back into the ellipse to pass through $F_2$. The point $P$ can be found based on this reflection process, as follows. Reflect $F_1$ about the line, and connect the reflected point $F_1'$ with $F_2$ to find the intersection of this line segment $F_1' F_2$ with the line $x+y=2$.

The reflection of $F_1(2,3)$ into the line $x+y=2$ is the point $F_1'(x',y')$ such that the midpoint of $F_1 F_1'$ lies on the line $x+y=2$, and the segment $F_1 F_1'$ is perpendicular to the line $x + y = 2 $. The first condition means

$ \dfrac{1}{2} [ (2 + x') + (3 + y') ] = 2 $

And the second condition means

$ \dfrac{ y' - 3}{x' - 2} = 1 $

So that, now we have the following linear system in $x'$ and $y'$

$ x' + y' = -1 $

$ x' - y' = -1 $

The solution is, by inspection, $F_1' = (x',y') = (-1, 0) $

Now the line segment $F_1' F_2 $ has the equation

$ y = \dfrac{5}{4} \ ( x + 1 ) $

The intersection of this line with $x + y = 2$ is the point $P = (\dfrac{1}{3}, \dfrac{5}{3} ) $

This point is on the ellipse, therefore,

$ 2 a = \| PF_1 \| + \| PF_2 \| = \dfrac{1}{3}\bigg( \sqrt{ 5^2 + 4^2} + \sqrt{ 8^2 + 10^2 } \bigg) = \sqrt{41} $

And

$| F_1 F_2 | = 2 c = \sqrt{ 1^2 + 2^2} = \sqrt{5} $

but

$ c = a e $

So the eccentricity $e$ is

$ e = \dfrac{c}{a} = \dfrac{2c}{2a} = \dfrac{ \sqrt{5} }{\sqrt{41}} $

Hence,

$ \dfrac{1}{e^2} = \dfrac{ 41 }{5} $

This Sage worksheet depicts the ellipse and the tangent line $x+y=2$.