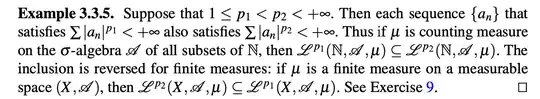Demonstration that $\boldsymbol{\ell^{p_1} \subseteq \ell^{p_2}}$ for $\boldsymbol{1 \leq p_1 < p_2 < \infty}$

Question

I was learning $L^p$ space from the book $\color{blue}{\textit{Measure Theory (2nd ed.)}}$ written by Donald L. Cohn. In Example 3.3.5, it shows us the crucial dependency of the relationship between $L^p$ spaces on the nature of the measure (Counting measure vs Finite measure).

I was curious about the following statement:

Suppose that $1 ≤ p_1 < p_2 < \infty$. Then each sequence $(a_n)$ that satisfies $\sum_{n=1}^{\infty} |a_n|^{p_1} < \infty$ also satisfies $\sum_{n=1}^{\infty} |a_n|^{p_2} < \infty$.

It might be a subtle problem, but I wonder how to show this convergence statement rigorously. I could understand it a little bit since if $\sum_{n=1}^{\infty} |a_n|^{p_1} < \infty$, then the power of this series should be finite. But I fail to formulate my idea.

Any help or any other idea w.r.t the statement would be appreciated!

Answer 1

Suppose $\sum |a_n|^{p_1} < \infty$.

Then $\sum_{|a_n|<1} |a_n|^{p_2} \leq \sum_{|a_n|<1} |a_n|^{p_1} < \infty$.

Furthermore, $|a_n|^{p_1} \geq 1$ for at most finite $n$ else $\sum |a_n|^{p_1} = \infty$.

Then $|a_n|^{p_2} \geq 1$ for at most finite $n$.

Hence $\sum_{|a_n|<1} |a_n|^{p_2} < \infty$.

Put these two together to get the result.