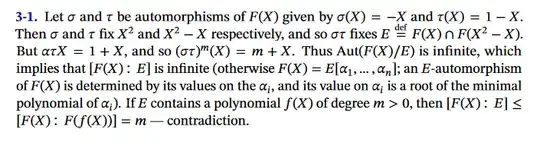The intersection $F(X^2)\cap F(X^2-X)$ for fields of characteristic zero

Question

I am trying to understand the solution to the following exercise from Milne's notes on Galois theory (available here):

At the end of the notes, the author presents the following solution to the problem:

Although I understand the argument, it is not immediately clear to me that this contradiction implies $F(X^2)\cap F(X^2-X)=F$. What immediately follows is that there are no polynomials of degree $m>0$ in this intersection. However, $E=F(X^2)\cap F(X^2-X)$ is a field of rational functions, so, in principle, it is not clear why there couldn't be non-constant rational functions $p(X)/q(X)$ in this field, even if there are no polynomials. More precisely, I can formulate my question as follows:

How to show that, if there exists $p(X)/q(X)\in E$, with $p, q$ coprime, $q(X)\neq0$, and $\deg(q)>0$, then there exists a polynomial of degree $m>0$ in $E$?

This way, we would demonstrate that $E$ indeed contains no non-constant rational functions and, therefore, $E=F$.

This reminds me of an older thread I happened to answer. Do the explanations there help you? — Jyrki Lahtonen, Jan 07 '24 at 05:26
If the intersection $E$ is bigger than $F$ then the intersection must be of the form $F(f(X)) $ (Luroth theorem) for some rational function $f(X) $ and then $[F(f(X)) :F(X)] $ is finite and has at most a finite number of automorphisms. — Paramanand Singh, Jan 07 '24 at 08:38
@ParamanandSingh The author of the notes has not yet presented Lüroth's Theorem in the chapter I am currently reading, but I will revisit the question later after becoming familiar with this result. Thanks! — Matheus Frota, Jan 09 '24 at 01:29

Zaran Zin · Answer 1 · 2024-04-13T12:58:05.707

1

$let f(x)=p(x)/q(x)$.So $f(x)q(x)-p(x)=0$ is the polynomial that x satisfies on F(f(x)).Then we have that $[F(x):F(f(x))] \leq max \{deg(q(x)),deg(p(x))\}$.So the extension is finite.

edited Apr 13 '24 at 12:58

answered Apr 13 '24 at 12:51

Zaran Zin

37

The intersection $F(X^2)\cap F(X^2-X)$ for fields of characteristic zero

1 Answers1