κ̄₀ for Mercury—Formula (BIS—Different definition of the term/angle)

Question

Following my other question about a specific “hidden” formula in Ptolemy’s model for Mercury, I am now looking for yet another “hidden” formula, this time the one used to find $\bar\kappa_0$ so that $OC=60$ in the figure below. We are given that $DC=60$ (in arbitrary units), that angles $AFD$ and $AEC$ are equal but of opposite direction (so $\angle AFD = -\angle AEC$), and that $OE=EF=FD$ (which is equal to 3, but I’d like to keep 3 out of the equation and just symbolize it by e (for “eccentricity”).

($A$ is the apogee of Mercury’s deferent centered on $D$. $D$ rides on the small circle centered on $F$. The Earth is at point $O$ [for “observer”]. Points $O$, $E$, and $F$ are always in a straight line with $A$. Mercury itself rides on the epicycle centered on $C$.)

While Ptolemy knew of absolutely no trigonometry and other modern mathematics, I don’t mind the answer to be expressed in modern terms, although simple trigonometry would be nice since math is not my forte.

P.S. I’ll also ask this question on AstronomySE.

Answer 1

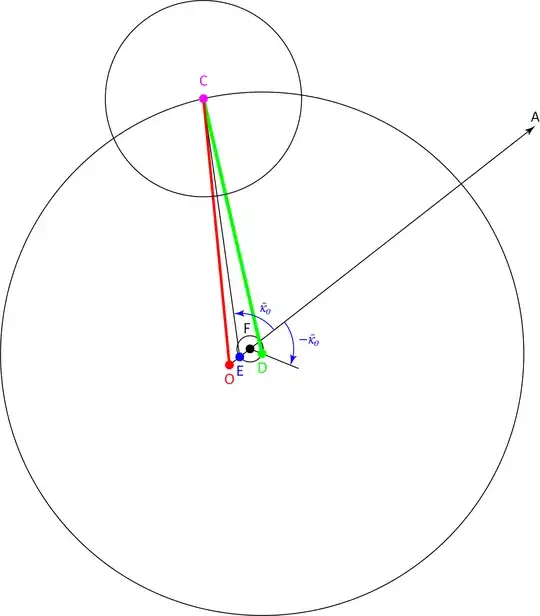
I got a quartic equation.

In the following, I'm going to show how I got the quartic equation.

Let $x:=\bar{\kappa_0}$ and $c:=\cos x$.

Let $G$ be the intersection point of $EF$ with $CD$.

Let $H$ be a point on $EF$ such that $DH\perp EF$.

Let $I$ be a point on $EF$ such that $CI\perp EF$.

Applying the law of sines to $\triangle{CEO}$, we have $$\frac{60}{\sin(180-x)}=\frac{e}{\sin C}=\frac{CE}{\sin(x-C)}$$ So, $$CE=\sqrt{3600-e^2(1-c^2)}-ec\tag1$$

Applying the law of sines to $\triangle{DFG}$, we have $$\sin\angle{DGF}=\frac{e\sin x}{DG}\tag2$$

Applying the law of sines to $\triangle{CEG}$, we have $$\sin\angle{CGE}=\frac{CE\sin x}{60-DG}\tag3$$

From $(2)(3)$, we get $$\frac{e\sin x}{DG}=\frac{CE\sin x}{60-DG}$$ so $$DG=\frac{60e}{CE+e}\tag4$$

Applying the law of cosines to $\triangle{FDG}$, we have $$DG^2=e^2+FG^2-2\cdot e\cdot FGc$$ which can be written as $$DG^2-FG^2=e^2-2ecFG\tag5$$

Applying the law of cosines to $\triangle{CEG}$, we have $$(60-DG)^2=(e+FG)^2+CE^2-2CE(e+FG)c$$ which can be written as $$DG^2-FG^2=-3600+120DG+e^2+2eFG+CE^2-2CE(e+FG)c\tag6$$

From $(5)(6)$, we get $$e^2-2ecFG=-3600+120DG+e^2+2eFG+CE^2-2CE(e+FG)c$$ $$FG=\frac{-3600+120DG+CE^2-2ecCE}{-2ec-2e+2CEc}=\frac{-2 e c y^2 - 2 e^2 c y + y^3 + e y^2 - 3600 y + 3600 e}{(y + e) (2c y - 2e c - 2e)}\tag7$$ where $y:=CE$.

Since $\triangle{GHD}\sim\triangle{GIC}$, we have $$DH:CI=GH:GI\tag8$$ Since $DH=e\sin x,CI=CE\sin x$ and $GI=HI-GH=(EI-EH)-GH=CE\cos x-(EF+FH)-GH=CE\cos x-e-e\cos x-GH$, it follows from $(8)$ that $$GH=\frac{yce-e^2 -e^2c}{y+e}$$

So, we get $$FG=FH+GH=ec+\frac{yce-e^2 -e^2c}{y+e}\tag9$$

It follows from $(7)(9)$ that $$\frac{-2 e c y^2 - 2 e^2 c y + y^3 + e y^2 - 3600 y + 3600 e}{(y + e) (2c y - 2e c - 2e)}=ec+\frac{yce-e^2 -e^2c}{y+e}$$ So, $$4 e c^2 y + 2 e c y - 2 e^2 c - y^2 - 2 e y - 2 e^2 + 3600=0$$

which can be written as $$\sqrt{3600-e^2+e^2c^2}=\frac{e(4 c^3 + 4 c^2 + 1)}{4 c^2 + 4 c - 2}$$ Squaring the both sides, we finally get $$\color{red}{(32 e^2 - 57600)\cos^4\kappa_0 + (56 e^2 - 115200)\cos^3\kappa_0 + 4 e^2 \cos^2\kappa_0+(- 16 e^2 + 57600)\cos\kappa_0 + 5 e^2 - 14400=0}$$