I am looking for a way (or a proof of nonexistence) to represent $K_{3,3}$ in the following way:
Each vertex of the graph should be one convex polyhedron and each edge of the graph should be equivalent to two polyhedra sharing a face.
Any idea?
Asked
Active
Viewed 150 times
2
-
In this MSE answer I give a construction that represents $K_{n,n}$ for any $n$. – Misha Lavrov Dec 30 '23 at 16:51
-
@MishaLavrov Could you explain a bit more? I didn't get how that is a solution to this problem. – MR_BD Jan 02 '24 at 18:41
-
If you take the picture here with three red polyhedra and three blue polyhedra, you get a representation of $K_{3,3}$. – Misha Lavrov Jan 02 '24 at 19:13
-
(Here is what that would look like.) – Misha Lavrov Jan 02 '24 at 19:21
1 Answers
3
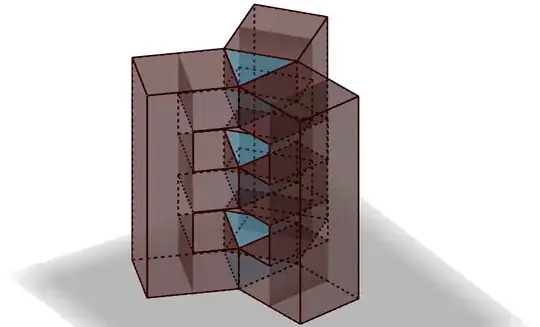Would this work for you? Three triangular prisms touched by three E-prisms. A similar construction should work for all graphs $K_{n,m}$.
EDIT: I gave this answer before there was the requirement that the polyhedra be convex. Some modifications can save this solution, though. Keep the middle triangular prism. Instead of E-prisms attach regularly decagonal prisms to the rectangular side. They have to be oriented so that the normal vectors on the decagonal faces point around the structure. The normal vectors on the rectangular faces point up, down, outward, and to the middle of the structure. (Think: Three coins standing on their rims, all rims touching in the middle. Not: Three coins lying down.) The remaining two triangular prisms are replaced by truncated pyramids. If the triangular prism in the middle touches the lateral rectangle number $n$ of a decagonal prism, the truncated pyramids touch lateral rectangles number $n \pm 2$.
Tzimmo
- 3,166