3

If $x^2+bx+a=0, x^2+ax+b=0$ do not have distinct real roots then find the maximum value of $\frac{a^2+b^2}{a+b}$ if $a,b\gt0$

Solution:

$D\le0\implies b^2-4a\le0, a^2-4b\le0$

It implies $b^2+a^2\le4(a+b)\implies \frac{b^2+a^2}{a+b}\le4$

So, the maximum value is $4$.

Is everything okay with both the question and the answer?

aarbee
  • 10,749
  • It looks ok. You think there is any problem? – NN2 Dec 27 '23 at 12:53
  • It would be better if you gave an example. ($a=b=4$) – youthdoo Dec 27 '23 at 12:58
  • @NN2 a friend insists that there is an inconsistency here. I don't see any. He would mention that inconsistency tomorrow. I'll try to update here then. – aarbee Dec 27 '23 at 13:02
  • 1
    Always remember that you've only calculated an upper bound. To show that it's truly a maximum, you need to explain why equality can hold. Hence, everything is NOT okay. – Calvin Lin Dec 27 '23 at 16:15
  • @CalvinLin yes, this is what my friend says is the inconsistency, that the maximum value is attained only when we have just one equation, not two i.e. when $a=b$ – aarbee Dec 28 '23 at 06:05

2 Answers2

3

This solution looks correct, but the only thing I might add is what @youthdoo alluded to. For what values of $a$ and $b$ do you attain the maximum value of 4? The max is attained when $D=0$ which gives the system of equations: $$(1)\ \ b^2 = 4a$$ $$(2)\ \ a^2 = 4b.$$

Dividing the two equations we obtain: $$\frac{b^2}{a^2} = \frac{a}{b} \implies b^3 = a^3 \implies a^3 - b^3 = 0.$$ Factoring we get $(a-b)(a^2+ab+b^2)=0.$ The only solution is $a=b$ since $a,b>0$. Plugging this back into one of the equations of the system we get $a=b=4$.

Matthew Albano
  • 171
1

As pointed in the comments, I overlooked some details in my previous answer. I am editing it to reflect on some relevant points.

We already know an upper bound for the expression is $4$.

In short, you can represent these inequalities as parabolas in the $1$st quadrant.

$$b^2-4a \le 0$$ $$a^2-4a \le 0$$ $$(a-2)^2+(b-2)^2 = (2\sqrt{2})^2$$

You can interpret the first two inequalities as parabolas and the third as a circle.

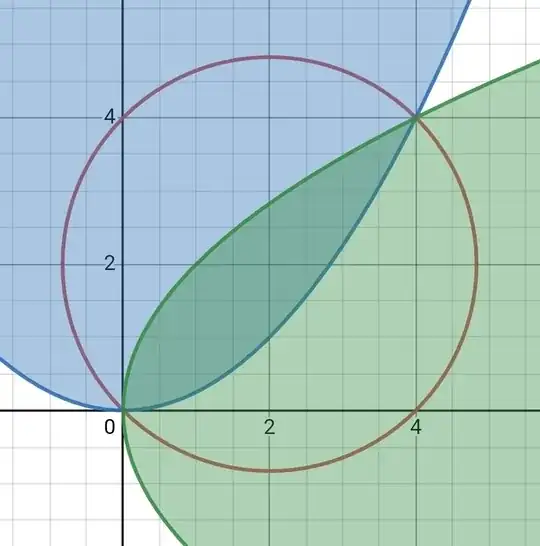
Geometrical representation

To find a maximum, you need to consider points that lie in the region that satisfies the first two inequalities (which is just the region inside the two parabolas), and are closest to the circle described by the third equation.

It is easy to see that in this case the upper bound $4$ is achieved with $(4,4)$.

But if you want distinct equations, you can try to find points with distinct values for the $x$ and $y$ coordinate. Clearly, there is no maximum in this case, but only a strict upper bound of $4$.

If you consider the problem over the distinct integers, this condition is achieved with $(2,1)$ only.

Sahaj
  • 5,355
  • Wonderful answer, thanks a lot. – aarbee Dec 28 '23 at 10:29
  • You need to uncheck this answer. It is not correct because it ignores the condition that each of the parabolas should not have distinct real roots. You can check on Desmos for yourself that at least one of the parabolas crosses through the $x$-axis with the given examples. And I don't mean tangentially. – Matthew Albano Dec 28 '23 at 13:42
  • Good catch. One of the two equations will not have distinct real roots – Sahaj Dec 28 '23 at 13:55
  • Additionally, the case where each of the parabolas have two complex roots will never achieve the max of $4$ because then this would amount to strict inequality for both quadratics: $D<0$. This implies $\frac{a^2 +b^2}{a+b}<4$. Furthermore, even if we grant $D<0$ for the first and $D \leq 0$ for the second we still cannot combine the inequalities as would want. The case of $D=0$ for both is the only one that works. – Matthew Albano Dec 28 '23 at 13:59
  • 1
    @MatthewAlbano thanks for the inputs. Means a lot. – aarbee Dec 29 '23 at 05:35