2

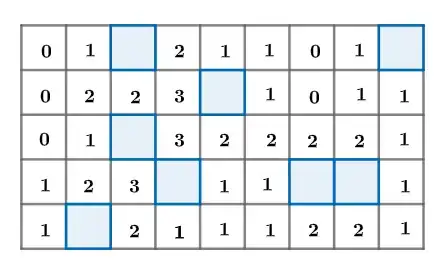
In the m*n grid paper, there are several shadow grids of any number and position distributed in the grid paper.

Q: If the number of the blank cell is the number of shaded cells around the cell (8 directions), What is the maximum sum of all the numbers in the square paper? For example,

enter image description here

In this picture, the sum of all the numbers is $5\times0+18\times1+11\times2+3\times3=49$

I came up with this question because I was playing Minesweeper, and I thought that the best situation would be one line of shadows, one line of blank space, and alternate lines. I have tested this conjecture, and it satisfies me without exception.

I don't have a good idea of how to solve this problem, maybe it's a problem of composition and graph theory, I don't think I've found a good idea so far. Can anyone help me with this problem? Thank you！

RobPratt
  • 50,938
spacedog
  • 443
  • 1
    It seems like this might already be addressed by this older question: https://math.stackexchange.com/q/807523/137524. But it's not evident to me whether the answers addresses the maximum value in all cases. – Semiclassical Dec 26 '23 at 14:36
  • @Semiclassical Wow, it turns out that this same problem existed a long time ago, but it still seems to be a problem to solve, only to estimate the upper and lower bounds. – spacedog Dec 26 '23 at 14:44
  • 1
    Can you [edit] the question to explain what is meant by a "shadow grid" and "shaded cell"? – D.W. Dec 26 '23 at 22:05

0 Answers0