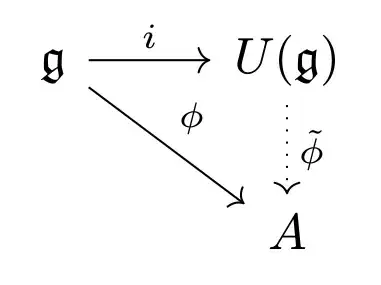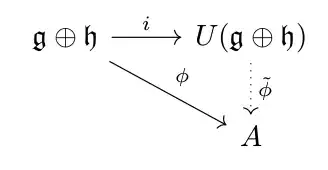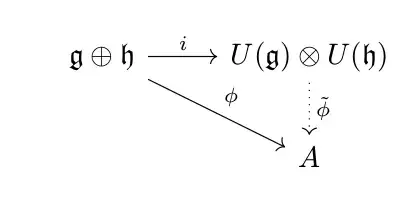How do I prove $U(\mathfrak{g} \oplus \mathfrak{h})\cong U(\mathfrak{g})\otimes U(\mathfrak{h})$ using the universal properties?

Question

Reading lecture notes on Hopf algebras, I came across a statement (which was heavily used by the author without a proof) that, given Lie algebras $\mathfrak{g}, \mathfrak{h}$, the universal enveloping algebra $U(\mathfrak{g}\oplus \mathfrak{h})$ is isomorphic to $U(\mathfrak{g})\otimes U(\mathfrak{h})$. I am trying to prove this statement using the universal properties of objects involved, namely, the universal property of the universal enveloping algebra

where $\phi$ is a linear map from $\mathfrak{g}$ to an associative unital algebra $A$ that respects the bracket, and $i$ is the canonical injection, which, in the case of the universal enveloping algebra of $\mathfrak{g}\oplus \mathfrak{h}$, reads as

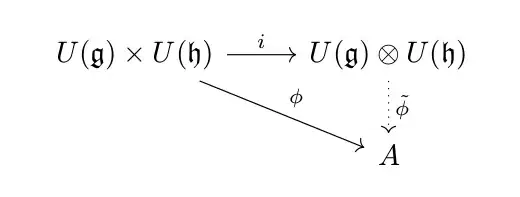
,and the universal property of tensor product of algebras

where $\phi, i$ are bilinear maps, $\tilde{\phi}$ is a morphism of associative algebras. So, theoretically, if we proved the following diagram:

i.e. that $U(\mathfrak{g})\otimes U(\mathfrak{h})$ satisfies the diagram for $U(\mathfrak{g} \oplus \mathfrak{h})$, we would have proved that $U(\mathfrak{g} \oplus \mathfrak{h}) \cong U(\mathfrak{g})\otimes U(\mathfrak{h})$. My line of reasoning is that we can inject $\mathfrak{g} \oplus \mathfrak{h}$ into $U(\mathfrak{g}) \times U(\mathfrak{h})$ linearly in each component, adding additional node and arrow to the diagram for tensor product:

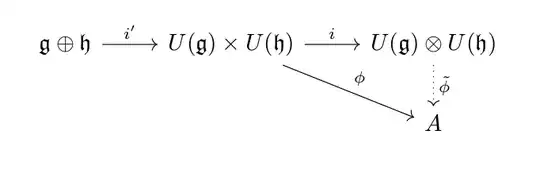
and then the compositions $i \circ i'$ and $\phi \circ i'$ would give us the desired diagram. Since I have very little experience working with diagrams and universal properties, I am not sure if my proof is correct, or how to make it rigorous. One of my concerns, for instance, is that in the diagram for the universal property of UEA, $i$ is specifically defined as the canonical injection; and canonical injection is defined into $U(\mathfrak{g}\oplus \mathfrak{h})$, not into $U(\mathfrak{g}) \otimes U(\mathfrak{h})$, so I am not sure if I can state that the two diagrams are "the same".

Answer 1

Let $k$ be the base field. What you should use is that $R\otimes_k S$ is a commutative co-product in the category of $k$-algebras. In other words, there are maps $i_R:R\to R\otimes_k S$ and $i_S:S\to R\otimes_k S$ such that for all $k$-algebras $A$, $$\operatorname{Hom}_{k-\text{alg}}(R\otimes_k S, A)\cong \operatorname{Hom}_{k-\text{alg}}(R,A)\times_{\text{Comm}}\operatorname{Hom}_{k-\text{alg}}(S,A)$$ where the natural mapping is given by pulling a map $\sigma:R\otimes_{k} S\to A$ back via $\sigma\circ i_R,\sigma\circ i_S$. The notation $\times_{\text{Comm}}$ means all pairs of $k$-algebra maps $\sigma:R\to A, \tau:S\to A$ such that $\sigma(x)\tau(y)=\tau(y)\sigma(x)$ for all $x\in R, y\in S$.

So what you need to do is prove that $U(\mathfrak{g}\oplus\mathfrak{h})$ is a commutative co-product of $U(\mathfrak{g}),U(\mathfrak{h})$ in the category of $k$-algebras. Now we have obvious injections (of Lie algebras) $$ \begin{split} \mathfrak{g}\to \mathfrak{g}\oplus\mathfrak{h}\quad g\mapsto (g,0)\\ \mathfrak{h}\to \mathfrak{g}\oplus\mathfrak{h}\quad h\mapsto (0,h) \end{split} $$ and from this you get maps $i_1:U(\mathfrak{g})\to U(\mathfrak{g}\oplus\mathfrak{h})$ and $i_2:U(\mathfrak{h})\to U(\mathfrak{g}\oplus\mathfrak{h})$ of $k$-algebras.

So lets look at the universal property. For any $k$-algebra $A$ and a map $\sigma:U(\mathfrak{g}\oplus\mathfrak{h})\to A$ of $k$-algebras we need to show that $$\operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{g}\oplus\mathfrak{h}), A)\cong \operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{g}),A)\times_{\text{Comm}}\operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{h}),A)\tag{1}$$ via the pullbacks $\sigma\circ i_1, \sigma\circ i_2$. Is it true? We know there are correspondences $$ \begin{align} \operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{g}),A)&\cong\operatorname{Hom}_{\text{Lie}}(\mathfrak{g}, A)\\ \operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{h}),A)&\cong\operatorname{Hom}_{\text{Lie}}(\mathfrak{h}, A)\\ \operatorname{Hom}_{k-\text{alg}}(U(\mathfrak{g}\oplus\mathfrak{h}),A)&\cong\operatorname{Hom}_{\text{Lie}}(\mathfrak{g}\oplus\mathfrak{h}, A) \end{align} $$ where $\operatorname{Hom}_{\text{Lie}}$ is in the category of Lie-algebras (over $k$) and $A$ is considered as a Lie algebra via the usual bracket in an associative algebra. So after tracing what all the maps and compositions are doing, the statement in $(1)$ is equivalent to $$ \operatorname{Hom}_{\text{Lie}}(\mathfrak{g}\oplus\mathfrak{h},A)\cong\operatorname{Hom}_{\text{Lie}}(\mathfrak{g},A)\times_{\text{Comm}}\operatorname{Hom}_{\text{Lie}}(\mathfrak{h},A)\tag{2} $$ where $\times_{\text{Comm}}$ in this context means all pairs of Lie maps $\sigma:\mathfrak{g}\to A, \tau:\mathfrak{h}\to A$ such that $[\sigma(x),\tau(y)]=0$ for all $x\in \mathfrak{g}, y\in\mathfrak{h}$.

Finally, $(2)$ follows from the fact that $\mathfrak{g}\oplus\mathfrak{h}$ is a commutative co-product in the category of Lie algberas over $k$, which it is because $\mathfrak{g},\mathfrak{h}$ commute inside $\mathfrak{g}\oplus\mathfrak{h}$.

Note that $\mathfrak{g}\oplus\mathfrak{h}$ being a commutative co-product in the Lie category is a stronger statement than $(1)$, because it means that $(2)$ holds for all Lie algebras placed there instead of $A$, and not just for Lie algebras coming from associative algebras!