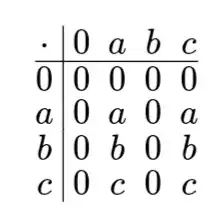1

Give an example of a non-commutative ring of order $4?$

I found an example as follows: Let $R=\{0,a,b,c\}$ with a binary operation + defined on it.

The multiplication table is given by:

enter image description here

Does this suffice as an example? Or do we need to define what the operation $+$ looks like explicitly? Precisely, do I need to write out an addition table just like the multiplication table above?

Thomas Finley
  • 3,625
  • If you want to define a ring, yes, you also need to define what + means in it. And, importantly, you need to make sure that + and * are distributive. (i.e. (x+y)z = xz + yz and x(y+z) = xy + xz; if the ring is not commutative, those are not equivalent) – Cecilia Dec 16 '23 at 03:29
  • @Cecilia Can you please help me define the operation of $+$ then? – Thomas Finley Dec 16 '23 at 03:35
  • 1
    As info: By your definition of ring, does your multiplication need to have a unit element? – Cecilia Dec 16 '23 at 03:44
  • @Cecilia No, not necessarily. – Thomas Finley Dec 16 '23 at 03:46
  • 1
    Recall that the addition of a ring forms an abelian group. There are only $2$ abelian groups of order $4$, and the cyclic group will always make your multiplication commutative. (Because of distributitvity). So there is only one possible way left the addition can work; then you'll have to adapt your multiplication to that addition. – Cecilia Dec 16 '23 at 03:53
  • The smallest ring (as opposed to a rng like here) has order eight. – Jyrki Lahtonen Dec 16 '23 at 06:15

0 Answers0