Why do cyclic inequality questions usually have three variables?

Question

This is probably more of a meta- or soft- question , but I thought I'd ask anyway. The question is the title:
Why do nearly all posts involving cyclic sums involve exactly three variables?

With only one or two variables, especially if the two variables have a constraint, perhaps the problem could be reduced to a single-variable calculus question.

I guess I'm wondering if with four or more, aside from the obvious chore of writing out all the terms, if there is some inherent lack of symmetry or 'niceness' present in the three-variable case that often rules them out. As an analogy, which is somewhat of a stretch, the cross-product is really only used in three dimensions. It exists in $\mathbb{R}^7$, and is rotationally invariant, but doesn't satisfy the Jacobi identity : there's something special about $\mathbb{R}^3$ specifically.

I was wondering if there was a similar symmetry or property involving cyclic sums in $n$ variables that is only present when $n=3$.

Answer 1

Here is my Soft-Answer to a Soft-Question.

SUMMARY : Cyclic Polynomials are not enough to generate all necessary terms with 4 or more variables.

When we have the given inequality , we eventually want to make it something like $(\cdots f(\text{n-variables}) \cdots)^2$ which must be at least $0$
In general , when we expand the Square & move the terms around , we will get the given inequality. This is high-level & overly-abstract & hand-wavey.

Now , when we have $0,1,2$ variables , Elementary Arithmetic & Differential Calculus will give Direct Answer & we have no necessity of Cyclic Polynomials.

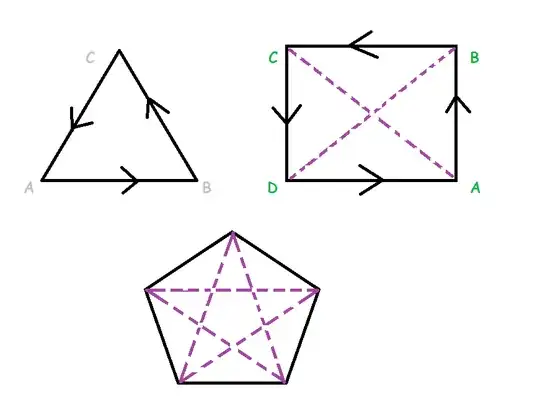
Consider 3 variables :
It will be like $(1+a+b+c)^2$ : where-ever necessary , we can include some Constant & Co-Efficient Eg $(2+3a+6b+9c)^2$ which I will ignore to keep it easy to visualize.

Expanding the Square , we will get 10 terms which we can club easily , $1+\Sigma a + \Sigma ab + \Sigma a^2$ , involving Cyclic Polynomials.

The Cyclic Polynomial occurs because every way to connect 2 variables occurs in the Cycle.
It will still work when we raise to Power 4 or 6.

Consider 4 variables :
It will be like $(1+a+b+c+d)^2$ : where I will ignore some Constant & Co-Efficient to keep it easy to visualize.

Expanding the Square , we will get 15 terms which we can try (unsuccessfully) to club , $1+\Sigma a + \color{red}{\Sigma ab} + \Sigma a^2$ , involving Cyclic Polynomials.

The Cyclic Polynomial is not enough because not every way to connect 2 variables occurs in the Cycle.
We will only get $ab,bc,cd,da$
We will not get $ac,db$

When we have 5 or more variables , more terms will be missing in the Cycle.
Hence Cyclic Polynomials are not enough.

Even more terms will be missing when we raise to Power 4 or 6.

In the Summations , we will have to use some thing more , that is , "all combinations of 2 variables" & "all combinations of 3 variables" & "all combinations of 4 variables" . . . .

SUMMARY : Cyclic Polynomials are not enough to generate all necessary terms with 4 or more variables.

When going beyond 3 variables , Cyclic Polynomial are no longer enough & we have to use Symmetric Sum Notation , which has a vast collection of theorems & Exercises . . . .

Answer 2

There are two sides of the question: Why do we need $3$ variables to express cyclic inequalities? Why are $3$ variables enough? Answers below are of course soft, and more general than the OP context.

• In algebraic topology, a circle $S^1$ is represented as (the border of) a $\Delta^2$ simplex, which has $3$ vertices. This means a cycle requires only $3$ points to be faithfully (from a topological viewpoint) represented.
• To represent the relation "a, b, c appear in that order in the cycle", we need a cyclic order relation, which is ternary (https://en.m.wikipedia.org/wiki/Cyclic_order#ref_ternary_relation).
• In elections, it is possible to have a population where a majority of people prefer A to B, a majority prefer B to C, and a majority prefer C to A (https://en.wikipedia.org/wiki/Condorcet_paradox). This non-intuitive, cyclic property appears as soon as there are $3$ elements to choose from, no need for more.
• A polygon can be triangulated, and functions be defined on vertices or edges, that are additive when juxtaposing triangles; which allows to reduce an expression on one $n$-vertices polygon to the sum of $n-2$ expressions on triangles, hence reducing problems with $n$ points to problems with $3$ points.
• Similarly, $3$-SAT is sufficient to express all SAT problems, with only a polynomial growth in complexity, so both are NP-complete; whereas 2-SAT problems can be solved in polynomial time. The link to cycles may seem far-fetched however: the reduction of SAT to 3-SAT involves decomposing any $n$-variables clause to a conjunction of $(n-2)$ $3$-variables clauses, by inserting new variables; this looks more like linear order than cyclic order.

Some of these properties generalize to higher dimensions and higher number of elements; some do not (e.g. triangulating an $n$-dimensional polytope into $\Delta^n$ simplexes is not always possible). However the new phenomena that would require more than $3$ elements would probably not be called "cyclic".
And perhaps our intuition (and taste) are not appealed by these higher-dimension situations: as an example there does not seem to be any study of spheric orders, that would require quaternary relations; similarly, in algebraic topology the fundamental group (which uses loops, hence $\Delta^2$, hence $3$ points) is much more used than higher-dimension homotopy groups.

Last but not least, there may be a sufficient number of interesting problems with $3$ variables, so that problems that require $4$ variables are seldom put forward. That's Occam's razor, or the principle of parsimony: we fancy more what can be expressed with the less entities.