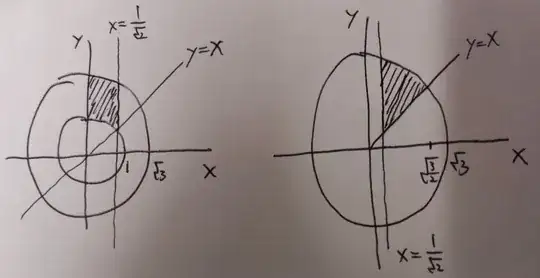3

I'm trying to crack an integral problem whose answer has been lost:

$$ I:=\int_0^\frac{1}{\sqrt{2}}\int_\sqrt{1-x^2}^\sqrt{3-x^2}\frac{x}{1+x^2+y^2}dydx+\int_\frac{1}{\sqrt{2}}^\sqrt{\frac{3}{2}}\int_x^\sqrt{3-x^2}\frac{x}{1+x^2+y^2}dydx$$

Judging from its form, I guess the method of polar coordinates might do the trick. Then I made a drawing to help find the limits of integration:

enter image description here

In this drawing, the left one is responsible for the first integral while the right one helps us take care of the second integral. With this drawing, I transformed the original question into one that reads: $$ I=\int_{\theta=\frac{\pi}{4}}^{\theta=\frac{\pi}{2}}\int_{r=1}^{r=\sqrt{3}}\frac{r\cos\theta}{1+r^2}rdrd\theta+\int_{\theta=\frac{\pi}{4}}^{\theta=\cos^{-1}\frac{1}{\sqrt{6}}}\int_{r=\frac{\cos\theta}{\sqrt{2}}}^{r=\sqrt{\frac{3}{2}}\cos\theta}\frac{r\cos\theta}{1+r^2}rdrd\theta$$

As it looks quite ugly, I have little confidence in what I just obtained. Does anyone get the same result? Thank you.

Sine of the Time
  • 8,579
Boar
  • 357
  • 2
    why it looks ugly? The integrals are separable (don't know if it's the right term) – Sine of the Time Dec 09 '23 at 11:05
  • If you add the two integrals you get an integral over the region $1 \le r \le \sqrt{3}, , \frac{\pi}{4} \le \theta \le \frac{\pi}{2}.$ – JanG Dec 10 '23 at 18:58
  • @JanG Hello, what do you mean by adding the two integrals? Is it possible to glue the two regions together? Thank you. – Boar Dec 12 '23 at 06:50
  • 1
    Since the integrand is the same we can glue the two regions together. The union will be $1 \le r \le \sqrt{3}, , \frac{\pi}{4} \le \theta \le \frac{\pi}{2}$ (polar coordinates). – JanG Dec 12 '23 at 10:30
  • @JanG I see, you are integrating over an eighth of the annulus! My drawing is so rough that I couldn't understand what you meant at first. – Boar Dec 12 '23 at 11:00

1 Answers1

1

Thanks to JanG's valuable comment, we can see $$\begin{align} I&=\int_{\theta=\frac{\pi}{4}}^{\theta=\frac{\pi}{2}}\int_{r=1}^{r=\sqrt{3}}\frac{r\cos\theta}{1+r^2}rdrd\theta=\left[\int_{1}^{\sqrt{3}}\left(1-\frac{1}{1+r^2}\right)dr\right]\cdot\left[\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\cos\theta d\theta\right]\\ &=\left[r-\tan^{-1}r\right]_{1}^{\sqrt{3}}\cdot\left[\sin\theta\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}=\left[(\sqrt 3-1)-(\frac{\pi}{3}-\frac{\pi}{4})\right]\cdot\left(1-\frac{\sqrt 2}{2}\right). \end{align}$$ The computation above suggests my original result will differ from the actual value by an extra integral (the second one).

Sine of the Time
  • 8,579
Boar
  • 357