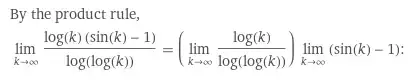7

Its known that $$ \sum_{n=1}^{\infty}\frac{1}{n^\alpha}$$ converges with $\alpha > 1$. But how does something like

$$\sum_{k=1}^\infty\frac{1}{k^{2-sin(k)}}$$ behave that gets close to 1 periodically?

The usual tests for convergence failed. Interestlingly I tried this logarithmic convergence criteria I found on german wikipedia. I states that if the series $$b_k=\frac{ln(k^{sin(k)-1})}{ln(ln(k))}$$ converges to something stricly smaller that $-1$ the series converges. Now i pluged this into wolframalpha and it outputs $-\infty$. But looking at the step-by-step soltion it seems to make a mistake. It applies the product rule for limits wrong IMO.

enter image description here

Lost
  • 147
  • 1
  • 11
  • 1
    I am pretty sure that something like condition 2 in this answer will work to show that the given series is divergent. – Sarvesh Ravichandran Iyer Nov 28 '23 at 10:32
  • 1
    This is not a trivial problem. there is an article here that give a rather general convergence test for series with positive terms. It is applied to $\sum_n\frac{1}{n^{2+\cos n}}$ and I think the same idea will work for your series. It does involve facts about density of $\sin n$ in $[-1,1]$ and properties of the number $\pi$. – Mittens Nov 29 '23 at 02:04
  • You may be interested in this question ("Is the series $\sum_{n=1}^\infty\frac{|\sin(n)|^n}n$ convergent?"). – Alex Ravsky Dec 10 '23 at 16:54
  • Related: https://math.stackexchange.com/questions/2626391/convergence-or-divergence-of-sum-n-1-infty-frac1n2-cos-n?noredirect=1. – Gonçalo Dec 13 '23 at 03:32

0 Answers0