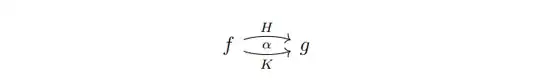I will give as mentioned above a description of a model of the $\infty$-category of chain complexes, by turning for any ring $R$ the category $\mathrm{Ch}_R$ of chain complexes of $R$-modules into a simplicially enriched category, and even a $\mathsf{Kan}$-enriched category (i.e. all hom simplicial sets are Kan complexes). (This is not a model for the derived $\infty$-category $\mathcal{D}(R)$.) Then we will see that homotopies between homotopies are what you'd expect them to be based on topological intuition.
For $n\geq 0$, we let $C^\Delta_{\mathrm{nd}}(\Delta^n)$ be the chain complex which is given in degree $m$ by $R[\{\text{non-degenerate $m$-simplices of $\Delta^n$}\}]$ and whose differential in degree $m$ is $\Sigma_{i=0}^m(-1)^i d_i$, with $d_i$ the boundary operator of simplicial sets. For $C,D\in\mathrm{Ch}_R$, we define a simplicial set $\mathrm{F}(C,D)$ by $\mathrm{F}(C,D)_n=\mathrm{Ch}_R(C\otimes C^\Delta_{\mathrm{nd}}(\Delta^n),D)$. One can verify that this is a Kan complex (because it is a simplicial $R$-module), and this defines a $\mathsf{Kan}$-enrichement on $\mathrm{Ch}_R$. From now on, when writing $\mathrm{Ch}_R$ we will understand it to carry this enrichement.
Note that $C^\Delta_{\mathrm{nd}}(\Delta^1)$ is the usual interval chain complex
$$
\require{AMScd}
\begin{CD}
\ldots@>>>0@>>>R@>{1\mapsto (1,-1)}>>R\oplus R@>>>0@>>>\ldots
\end{CD}
$$
with the term $R\oplus R$ in degree 0. We already know that a chain homotopy from $f\colon C\to D$ to $g\colon C\to D$ is a map $H\colon C\otimes C^\Delta_{\mathrm{nd}}(\Delta^1)\to D$ with the following property: the two inclusions $0,1\colon\Delta^0\to\Delta^1$ give us compositions $$C\cong C\otimes C^\Delta_{\mathrm{nd}}(\Delta^0)\xrightarrow{\mathrm{id}\otimes 0_*} C\otimes C^\Delta_{\mathrm{nd}}(\Delta^1) \xrightarrow{H} D$$ and $$C\cong C\otimes C^\Delta_{\mathrm{nd}}(\Delta^0)\xrightarrow{\mathrm{id}\otimes 1_*} C\otimes C^\Delta_{\mathrm{nd}}(\Delta^1) \xrightarrow{H} D,$$ and we require these maps to be given by $f$ and $g$, respectively. See this nLab page, Proposition 3.2 for a proof that this is the same data as your definition of a chain homotopy.
This notion of homotopy is the same as a homotopy from $f$ to $g$ in the $\mathsf{Kan}$-enriched category $\mathrm{Ch}_R$. Thus for the notion of a homotopy between homotopies, we look at the corresponding notion in the world of simplicial categories. Given a general simplicial category $\mathcal{C}$, two maps $f,g\colon x\to y$ in it, and two homotopies $H,K\colon f\to g$ in it, there are three sensible definitions of what a homotopy $\alpha\colon H\to G$ is, which are all equivalent as far as homotopy theory is concerned. The three possibilities are:
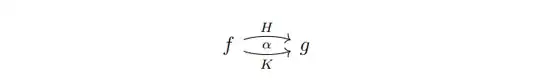
- $\alpha$ is a diagram as above, interpreted as a map $\alpha\colon W\to \mathcal{C}(x,y)$ (plus boundary conditions), where $W=\Delta^2/\Delta^{\{0,1\}}$ is the 2-simplex where we collapse the first edge to a point.
- $\alpha$ is a diagram as above, but interpreted as a map $\alpha\colon W'\to \mathcal{C}(x,y)$ (plus boundary conditions), where $W'=\Delta^2/\Delta^{\{1,2\}}$ is the 2-simplex where we collapse the last edge to a point.
- $\alpha$ is a commutative square
$$
\require{AMScd}
\begin{CD}
f @>{H}>> g\\
@V{\mathrm{id}}VV @VV{\mathrm{id}}V\\
f @>>{K}> g
\end{CD}
$$
in the simplicial set $\mathcal{C}(x,y)$. So we now look at maps $\alpha\colon\Delta^1\times\Delta^1\to\mathcal{C}(x,y)$ satisfying the appropriate boundary conditions. We can define a simplicial set $Z$ obtained from $\Delta^1\times\Delta^1$ by first collapsing $\Delta^1\times\{0\}$ to a point, and then collapsing $\Delta^1\times\{1\}$ to a point. We can avoid stating the identity boundary conditions by just immediately looking at maps $\alpha\colon Z\to\mathcal{C}(x,y)$ (plus boundary conditions about $f, g, H$ and $K$).
Note that $Z=W\sqcup_{\Delta^1} W'$, so a homotopy in the sense of 3. is just the data of an extra map $h\colon C\to D$, and then two homotopies in the sense of 1. and 2. from $h$ to $f$ and from $h$ to $g$. Since homotopies are reversible and since homotopies may be taken to be identities, you may believe that all three notions above give you the same theory. We only study what 1. looks like concretely in our case, since symmetry and the preceding discussion will tell you what the other homotopies look like in our case, and since these other notions give you the same theory of homotopies (in some precise sense).
The assignment $C^\Delta_\mathrm{nd}\colon\Delta\to\mathrm{Ch}_R$ can be extended via left Kan extension to a colimit-preserving functor $C^\Delta_\mathrm{nd}\colon\mathsf{sSet}\to\mathrm{Ch}_R$ (which is also the left adjoint in the Dold-Kan correspondence in case $R=\mathbb{Z}$; see Theorems 2.1 and 2.2 on this nLab page, although this is not immediately clear from our description; also maybe this also is the correct functor for general $R$, but I am not going to think about this now). We now see that, for a simplicial set $X$, there is a bijection $\mathsf{sSet}(X, \mathrm{F}(C,D))\cong\mathrm{Ch}_R(C\otimes C^\Delta_\mathrm{nd}(X), D)$ which is natural in all variables. Namely, the bijection holds by definition for $X=\Delta^n$, and both sides are colimit-preserving in $X$.
Therefore, a map $\alpha\colon W\to\mathrm{F}(C,D)$ is the same data as a map $C\otimes C^\Delta_\mathrm{nd}(W)\to D$ of chain complexes. A computation shows that $C^\Delta_\mathrm{nd}(W)$ is the chain complex
$$
\require{AMScd}
\begin{CD}
\ldots @>>> 0 @>>> R @>{(-1, 1)}>> R\oplus R @>{A}>> R\oplus R @>>> 0@>>>\ldots
\end{CD}
$$
where $A(1,0)=(-1,1)=A(0,1)$, and the rightmost term $R\oplus R$ lives in degree 0. Another computation (albeit slightly tedious to get all the details correct) shows then that a map $C\otimes C^\Delta_\mathrm{nd}(W)\to D$ is precisely the first type of homotopy that Maxime mentiones in his answer (linked in the comment above), i.e. a map $\alpha$ of the appropriate type such that $\partial\alpha= H-K$ in the appropriate sense. By all means check this if you don't believe me, because I might have made mistakes in this computation. However, given that I arrived exactly at his notion of homotopy, it sounds plausible that it is correct.
Maxime also mentions the possibility of defining a higher homotopy $\alpha$ as a chain map $\alpha\colon C\otimes C^\Delta_\mathrm{nd}(\Delta^1)\otimes C^\Delta_\mathrm{nd}(\Delta^1)\to D$ satisfying certain boundary conditions. Unfortunately, $C^\Delta_\mathrm{nd}(\Delta^1)\otimes C^\Delta_\mathrm{nd}(\Delta^1)$ is not isomorphic to $C^\Delta_\mathrm{nd}(X)$ for any simplicial set $X$, but I suspect that you can find a meaningful relation with $C^\Delta_\mathrm{nd}(\Delta^1\times\Delta^1)$ or something like it. I'm interested in that, so if I have the time I will take a look at it tomorrow.