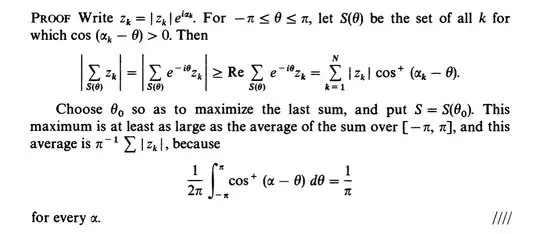4

I'm currently reading through Rudin's Real and Complex Analysis (3rd Edition) textbook and have stumbled upon a lemma which reads as follows:

6.3 Lemma If $z_1,...,z_N$ are complex numbers then there is a subset $S$ of $\{1,...,N\}$ for which $|\sum_{k\in s}z_k|\geq\frac{1}{\pi}\sum_{k=1}^{N}|z_k|$. [c.f. pg. 118].

The proof is a lot to type out, so I hope the image at the bottom is sufficient. However, the proof isn't necessarily what's of concern to me, this part makes perfect sense. What I'm confused on is the intuitive aspect: How could one go about visualizing this statement? Or at the very least explain it in a manner which is less logically-sound, and more intuitively sound? It's a very useful lemma which I'm shocked to have found no other articles on this site discussing. If somebody could attempt to clarify what's going here, I would greatly appreciate it! Thank you.

enter image description here

J.G.131
  • 1,098
  • Sorry for the nitpicking, would you mind changing $n$ to $N$? It's a very nice question! – Severin Schraven Nov 21 '23 at 19:55
  • 1
    “I'm shocked to have found no other articles on this site discussing” – What about https://math.stackexchange.com/q/967906/42969 and https://math.stackexchange.com/q/654840/42969 ? – Martin R Nov 21 '23 at 20:11
  • @SeverinSchraven Fixed it. Thanks for pointing that out! – J.G.131 Nov 21 '23 at 20:57
  • @MartinR This is certainly helpful, however I'm looking for an intuitive explanation as opposed to proofs. I'll nonetheless read through the alternate proofs you have provided to see if it makes any further intuitive sense, though I remain curious as to see what answers I can get on here. – J.G.131 Nov 21 '23 at 20:59
  • 2
    Here is another one with one geometric proof (with a weaker constant): https://math.stackexchange.com/q/91939/42969 – Martin R Nov 21 '23 at 21:08
  • if you are happy with a worse constant than $1/\pi$ the explanation is simple - if complex numbers are within a controlled angle so all their real (or all ther imaginary) parts are comparable to their modulus, so in other words $\cos \arg w >=\delta$ (or similar) for all, the inequality is obvious and by the pigeonhole principle we can always find a fixed fraction like that by splitting the plane into a few sectors – Conrad Nov 21 '23 at 21:09
  • 2
    And here is the generaliization to higher dimensions: https://math.stackexchange.com/q/102508/42969 – Martin R Nov 21 '23 at 21:10
  • @MartinR Great I'll look into these previously answered questions. Thank you! – J.G.131 Nov 21 '23 at 21:25

0 Answers0