I have an iterated integral with these two homework assignments on it :
(1) change the order of integration
(2) go to polar coordinates and set the limits of integration according to new ones variables.
I think I was able to solve both of these tasks, please tell me if I did it correctly? Thank you very much!
The iterated integral is:
$$\int_{0}^{1}dx\int_{x^3}^{x^2}f(x;y)dy$$
(1) change the order of integration
My answer is
$$\int_{0}^{1}dy\int_{\sqrt{y}}^{\sqrt[3]y}f(x;y)dx$$
Solve:
Let's find the inverse functions, taking into account the fact that we are in the first quarter of the Cartesian coordinate system
$y = x^2 = > x = \sqrt(y)$, $y = x^3 => x = \sqrt[3]{y}$
on the segment $0 \leq x \leq 1$
$$\sqrt{y} \leq \sqrt[3]{y}$$
(2) go to polar coordinates and set the limits of integration according to new ones variables
My answer is
$$\int_{0}^{\frac{\pi}{4}}d\phi\int_{\frac{sin(\phi)}{cos^2(\phi)}}^ {\sqrt{\frac{sin(\phi)}{cos^3(\phi)}}} f(r*cos(\phi); r*sin(\phi))r*dr$$
Solve:
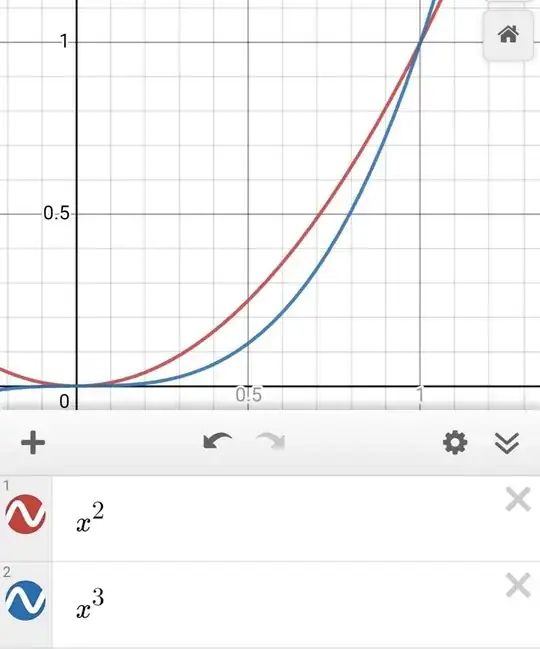
Since the outer integral in our case with $d\phi$, then we fix the angle and see how $r$ will change depending on it. We see that r goes from the red graph to the blue one.
Red to polar:
$$y = x^2$$
$$rsin(\phi) = r^2cos^2(\phi)$$
$$r = \frac{sin(\phi)}{cos^2(\phi)}$$
Blue to polar:
$$y = x^3$$
$$rsin(\phi) = r^3*cos^3(\phi)$$
$$r^2 = \frac{sin(\phi)}{cos^3(\phi)}$$
Choosing the positive
$$r = \sqrt{\frac{sin(\phi)}{cos^3(\phi)}}$$
We have found the boundaries and therefore can substitute them into our polar integral:
$$\int_{0}^{\frac{\pi}{4}}d\phi\int_{\frac{sin(\phi)}{cos^2(\phi)}}^
{\sqrt{\frac{sin(\phi)}{cos^3(\phi)}}}
f(r*cos(\phi); r*sin(\phi))r*dr$$