Evaluate :
$$\begin{equation} \iiint_{\Omega} z^{2} dV , \quad \Omega : x^{2} + y^{2} + z^{2} \leq R^{2}, \quad x^{2} + y^{2} \leq Rx \quad (R > 0). \end{equation}$$
I have solved the question , but my method was too ugly , could you please offer me some help of inspiring me of some elegant methods ?
Thank you !
My method is here :
Here is the plot of the corresponding region when $R = 1$ using Mathematica:
Based on it, I think that a change of coordinates to cylindrical coordinates would be interesting.
Hopefully this helps!
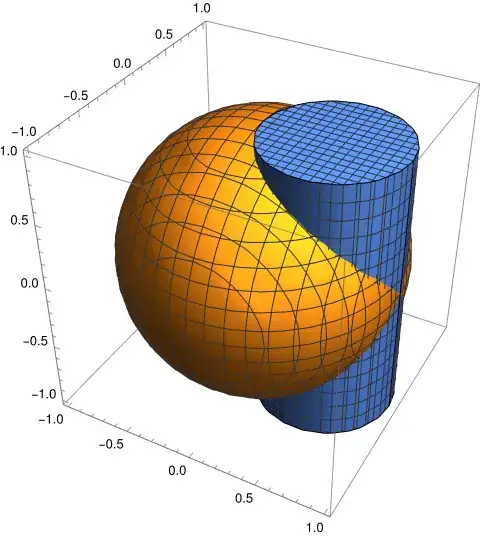
This integral works nicely in cylindrical coordinates. In the $xy$-plane the cylinder lies inside the sphere.
The equation of the cylinder is, in polar coordinates, $$ r\leq R\cos\theta,\qquad\qquad -\frac\pi2\leq\theta\leq\frac\pi2. $$ The cylinder is bounded above and below by the sphere, and so the integral becomes \begin{align} \iiint_\Omega z^2\,dV &=\int_{-\pi/2}^{\pi/2}\int_0^{R\cos\theta}\int_{-\sqrt{R^2-r^2}}^{\sqrt{R^2-r^2}}r\,z^2\,dz\,dr \,d\theta\\[0.2cm] &=\int_{-\pi/2}^{\pi/2}\int_0^{R\cos\theta}\frac23\,(R^2-r^2)^{3/2}r\,dr \,d\theta\\[0.2cm] &=\int_{-\pi/2}^{\pi/2}\frac2{15}\,(R^5-(R^2-R^2\cos^2\theta)^{5/2})\,d\theta\\[0.2cm] &=\frac{2R^5}{15}\int_{-\pi/2}^{\pi/2}(1-(1-\cos^2\theta)^{5/2})\,d\theta\\[0.2cm] &=\frac{2R^5}{15}\bigg(\pi-2\int_{0}^{\pi/2}(1-\cos^2\theta)^{5/2}\,d\theta\bigg)\\[0.2cm] &=\frac{2R^5}{15}\bigg(\pi-2\int_{0}^{\pi/2}\sin^5\theta\,d\theta\bigg)\\[0.2cm] &=\frac{2R^5}{15}\bigg(\pi-2\int_{0}^{1}(1-t^2)^2\,dt\bigg)\\[0.2cm] &=\frac{2R^5}{15}\bigg(\pi-\frac{16}{15}\bigg)\\[0.2cm] \end{align}
