I am reading the definition of Bialgebras over a field $\mathbb{K}$. The definition is the following:
A bialgebra over a field $\mathbb{K}$ is a vector space $B$ over $\mathbb{K}$ equipped with $\mathbb{K}$-linear maps (multiplication) $\nabla : B \otimes B \to B$, (unit) $\eta: \mathbb{K} \to B$, (comultiplication) $\Delta: B \to B \otimes B$, and (counit) $\varepsilon: B \to \mathbb{K}$ such that:
$(B,\nabla,\eta)$ is a unital associative algebra.
$(B,\Delta,\varepsilon)$ is a (counital, coassociative) coalgebra.
along with the following four compatibility conditions:
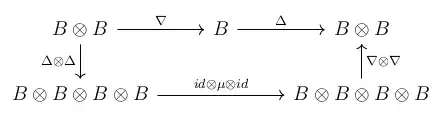
- Relation between multiplication $\nabla$ and comultiplication $\Delta$:
where $\mu: B \otimes B \to B$ is the linear map defined by $\mu(x \otimes y) = y \otimes x$ for all $x, y \in B$.
- Relation between multiplication $\nabla$ and counit $\varepsilon$ and comultiplication $\Delta$ and unit $\eta$:
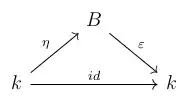
- Relation between unit $\eta$ and counit $\varepsilon$:
The four commutative diagrams can be read either as "comultiplication and counit are homomorphisms of algebras" or, equivalently, "multiplication and unit are homomorphisms of coalgebras".
My Question: How can we conclude the statement "comultiplication and counit are homomorphisms of algebras" from the above diagrams?