What is the asymptotic expansion of the integral $\int_{-\infty}^{\infty} \frac{\tanh{(x^2-a^2)}}{x^2-a^2} dx$ in the limit of large $a$?

Question

I am trying find the asymptotic form of the following integral for large $a$

$$ I(a) = \int_{-\infty}^\infty \frac{\tanh{(x^2-a^2)}}{x^2-a^2} dx.$$

Mathematica is unable to numerically integrate it due to the (removable) singularity at $x=\pm a$.

I removed the singularity by changing the limits from $0$ to $\infty$ (even function) and substituting $(x-a) = \pm e^t$ (on either sides of $x=a$). Afterwards, mathematica could numerically integrate it. I evaluated the integral for several values of $a$, and found that the integral has the asymptotic form $I(a) \sim \frac{c_1}{a} + 4 \frac{\log a}{a}$, where $c_1 \approx 4.41015$.

How to find the analytical form of $c_1$?

Answer 1

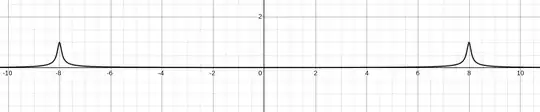
Plot of the integrand for $a=8$.

---

As the integrand is even, $I(a) = 2 \int_{0}^\infty \frac{\tanh{(y^2-a^2)}}{y^2-a^2} dy$

We can break the limits of integration into three intervals, $0 < y< a(1-\delta)$, $a(1-\delta) < y< a(1+\delta)$, and $a(1+\delta)<y<\infty$, where $\delta$ is chosen such that $\frac{1}{a} \ll \delta \ll 1$, so that $\tanh{(a \delta)} \approx 1$.

Then, the first part is, $I_1(a) = 2 \int_{0}^{a-a\delta} \frac{\tanh{(y^2-a^2)}}{y^2-a^2} dy \approx 2 \int_{0}^{a-a\delta} \frac{(-1)}{y^2-a^2} dy = \frac{1}{a} \log\frac{2-\delta}{\delta} \approx \frac{1}{a} \log\frac{2}{\delta}$.

The second part is, $I_2(a) = 2 \int_{a-a\delta}^{a+a\delta} \frac{\tanh{(y^2-a^2)}}{y^2-a^2} dy \approx 2 \int_{a-a\delta}^{a+a\delta} \frac{\tanh{(2a(y-a))}}{2a(y-a)} dy = \frac{1}{a} \int_{-2a^2 \delta}^{2a^2 \delta} \frac{\tanh{z}}{z} dz$.

Here I use the known result $\int_0^b \frac{\tanh x}{x} \approx C + \log b$, where $C = \gamma + \log(\frac{4}{\pi})$. Here $\gamma$ is the Euler's constant.

Then, $I_2(a) \approx \frac{2}{a} (C + \log(2 a^2 \delta))$.

The third part is, $I_3(a) = 2 \int_{a+a\delta}^{\infty} \frac{\tanh{(y^2-a^2)}}{y^2-a^2} dy \approx 2 \int_{a+a\delta}^{\infty} \frac{1}{y^2-a^2} dy = \frac{1}{a} \log\frac{2+\delta}{\delta} \approx \frac{1}{a} \log\frac{2}{\delta}$.

After adding everything, $\delta$ cancels, and we get,

$$I(a) = I_1 (a) + I_2(a) + I_3 (a) \approx \frac{2}{a} (C + 2 \log 2 + 2 \log a) = \frac{2\gamma + 2 \log(16/\pi) + 4 \log a}{a}.$$

The numerical value of $\boxed{c_1 = 2 \gamma + 2\log(16/\pi)}$ is approximately $4.41015$.