I recently posted on the solution to the nonlinear recurrence
$$ R_n=A+\frac{2AR_{n-1}}{2A+R_{n-1}} $$
Presently, I am exploring negative indices, analytic continuation, and complex parameters (here, there is single parameter, $R_0$). A big surprise ensued.
In this problem, the parameter $A$ is superfluous and can taken as unity WLOG. The above equation can then be written as
$$ R_n= \frac{3R_{n-1}+2}{R_{n-1}+2} $$
This is seen to be a particular case of the First-order Rational (or Ricatti) Difference Equation, namely,
$$ R_n= \frac{aR_{n-1}+b}{cR_{n-1}+d} $$
And you can readily determine the negative index solution from
$$ R_n= \frac{-dR_{n+1}+b}{cR_{n+1}-a} $$
Solutions to the Ricatti difference equation are well known, and in the present case it turns out to be
$$ R_n= \frac{2c_04^n+1}{c_04^n-1},\quad c_0=\frac{R_0+1}{ R_0-2},\quad n\in[0,N] $$
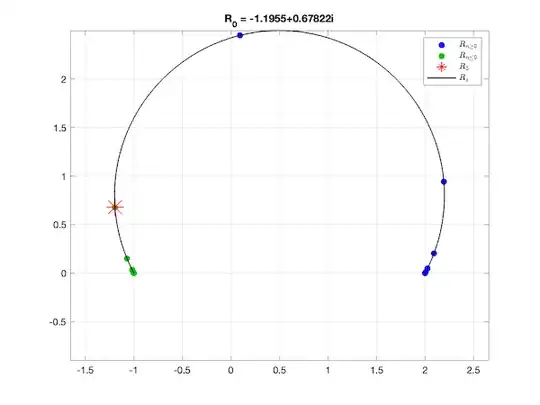
and similarly for negative indices. Now, I’m interested in looking at the sequence for positive and negative indices and the analytic continuation, call it $R_x$, for $x\in[-N,N]$. The first figure below shows the positive and negative indices in blue and green dots, respectively. The red asterisk is $R_0$, and the solid line is $R_x$. Notice that
$$ \lim_{n\to\infty}R_n=2 \\ $$ $$ \lim _{n\to-\infty}R_n=-1, $$
as you would expect from the recurrence relation.
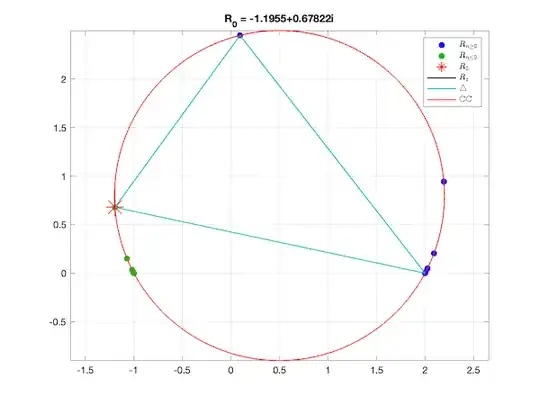
Insofar as this resembles a circular arc, I tested the idea as follows: A triangle was created from three points in the recurrence and the circumcenter and radius were determined. The second figure below shows the triangle (cyan) and circumcircle (red), which is seen to pass through all points of the recurrence. Unfortunately, I cannot see how a circle, say $z-z_0=re^{i\theta}$, arises out of the above solution for $R_x$. There is only a single complex constant there, $c_0$.
What I did
I took the above solution (in terms of $x$) and multiplied the numerator and denominator by the conjugate of the denominator. You end up with a solution of the form
$$ R_x=\frac{A(x)+B(x)}{C(x)} $$
where
$$ A(x)=(2c_0+c_0^*)4^x $$
$$ B(x)=2c_0c_0^* 4^{2x}+1 $$
$$ C(x)= c_0c_0^* 4^{2x}-(c_0+c_0*)4^x +1 $$
Here, $A(x)$ is the only complex term. And here I am stuck as I cannot see how this translates to a circle in the complex plane.
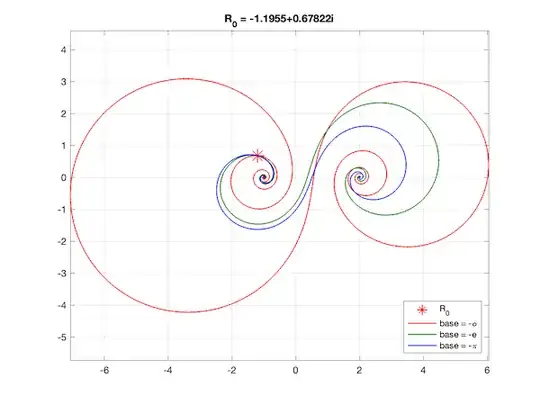
Here are some additional observations of these curves in the complex plane, The above results are for a base of 4 raised to the power $n$ (or $x$). Taking this a a toy model, we can inquire what happens when the base is changed. We find that the radius of the circle depends only upon $R_0$, and the terms of the recurrence lie on the same circle, albeit at different locations, for all positive values of the base.
Not so, however, for negative values of the base. Here we find compound spirals that have only in common that they pass through the same initial condition, $R_0$. The third figure below shows a comparison of curves for bases of $-\varphi,\ -e$, and $-\pi$.