1

The range of $\sin^{-1}(x)$ is (-$\pi/2, \pi/2)$, so is that of cosec$^−$$^1$(x) {except the 0 since 1/0 isn't defined}

The range of $\cos^{-1}(x)$ is (0, $\pi)$, so is that of $\sec^{-1}(x)$ {except the $\pi/2$ since 1/0 isn't defined}

Why isn't the same true for $\tan^{-1}(x)$ and $\cot^{-1}(x)$?

Why is the range of $\tan^{-1}(x)$ = (-$\pi/2, \pi/2)$ but that of $\cot^{-1}(x)$ = (0, $\pi)$

aren't they reciprocals?

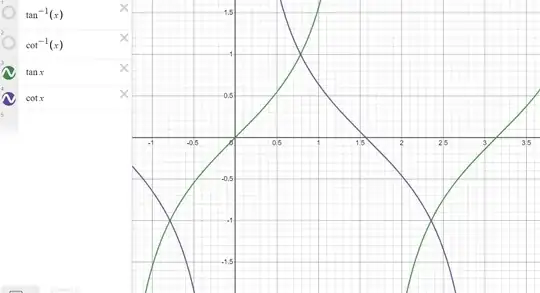
enter image description here

from the graph, it's clear that that would be possible too (i.e. they can have the same range too, except cot$^−$$^1$(x) would not have the 0 for obvious reasons)

Ricky
  • 3,194
Maddy
  • 87
  • 1
  • 8
  • It is, in Wolfram Alpha or if you define $\tan^{-1}(\frac1x)=\cot^{-1}(x)$. There are different conventions – Тyma Gaidash Nov 05 '23 at 14:02
  • because $\cot (\theta) = \frac{\cos (\theta)}{\sin (\theta)}$. And $\sin(\theta) = 0$ when $\theta = 0$ and $\theta = \pi$ – Miranda Nov 05 '23 at 14:20
  • Extending the comment of @Miranda, note that the range of the arctan function, $~-\pi/2 < \theta < \pi/2,~$ matches the range of the arcsine function, except for its endpoints. So, you would expect the range of the arccot function to match the range of the arccos function, excepting its endpoints, which is $~0 < \theta < \pi.$ – user2661923 Nov 05 '23 at 16:23
  • and why would I expect that @user2661923? only because they are in the numerator? Well, arcsec matches the range of arccos, as I mentioned in the question. Wouldn't arccot match the range of arcsin by that logic? My only point of this argument was that it would be so convenient (and it works too) for the principal domain of the cot function to match that of the tan function, only because they are reciprocals, just like all other trig functions do. – Maddy Nov 06 '23 at 12:29
  • Tangent is sine/cosine. So, arctan function's range matches the range of the inverse function, arcsine, that corresponds to the numerator of the tangent function. Exception is that endpoints excluded, because you can't have the denominator, cosine, equal to zero. Perfectly analogous logic focuses on cotan = cos/sine, so range of arccot function should match range of arccos function, with endpoints excluded, since (again), you can't have denominator (in this case the sine function) equal to zero. ...see my next comment – user2661923 Nov 06 '23 at 12:33
  • for instance, say you want arccot(-sqrt(3)), wouldn't things be easier to say that is equal to arctan(-1/sqrt(3))=-$\pi$/6? But no, as per range 0 to $\pi$, the actual value would be $\pi$-$\pi$/6=5$\pi$/6 – Maddy Nov 06 '23 at 12:34
  • So, the way to analyze what to expect for the range of the arccot function is to go back to basics. First, you have to determine why the range of the arcsine and arccos functions are what they are. Then, you have to analyze how the range of the arctan function evolved. Then, you have to apply the same logic to determine how the range of the arccot function should evolve. – user2661923 Nov 06 '23 at 12:35

2 Answers2

2

I don't have enough reputations to comment, hence I am commenting as an answer.

I think it is defined in such a way so that the domain has minimum discontinuity. I feel that the advantages of minimizing discontinuity must be greater than the disadvantages of the domain not matching tan inverse.

Also, defining like this provides the additional advantage of writing $\tan^{-1}x + \cot^{-1}x = \frac{\pi}{2}$.

Gary
  • 36,640
SemiballisticS
  • 25
1

Notice that $$\tan(\tfrac\pi2)=\tan(-\tfrac\pi2)=\pm\infty$$ and $$\tan x:(-\tfrac\pi2,\tfrac\pi2)\to\Bbb R$$ is a bijective function so that it is has an inverse $$\arctan x:\Bbb R\to (-\tfrac\pi2,\tfrac\pi2).$$

Similarly, notice that $$\cot0=\cot\pi=\pm\infty$$ and $$\cot x:(0,\pi)\to\Bbb R$$ is a bijective function so that it is has an inverse $$\operatorname{arccot}x:\Bbb R\to (0,\pi).$$

SemiballisticS mentioned about the additional advantage $$\arctan x+\operatorname{arccot} x=\frac\pi2.$$ But, he did not give the proof. I don't know if it is a good proof but my reasoning is as follows:

Let $\arctan x=\theta$. Then $\operatorname{arccot} x=\frac\pi2-\theta+k\pi$ for some integer $k.$ Now, if we take $x=0$ then $\theta=0$ and $\operatorname{arccot}0=\frac\pi2.$ So $k=0.$

Bob Dobbs
  • 15,712