How do I calculate the intersection points between inverse shared tangent lines, a circle, and a bounding box?

Question

Context

I am attempting to draw a polygon with 4 or 5 corners using a software library that draws shapes by taking in an array of corners in the form of $(X,Y)$. I am somewhat woefully under skilled in my understanding of geometry here, and looking for either the formulas to solve my problem or some good directions to tutorials, videos, and other learning tools, or both.

Givens

I have two circles defined by their centers and their radius $A_c, A_r, B_c, B_r$ and the bounding box extends from $(0,0)$ to some corner, $(BB_X,BB_Y)$.

This produces either eight or ten values I want to calculate. The shape I want is represented by the pink shaded area, and the points I need to produce it by the green stars.

The Question

What formulas do I use to calculate these 4 or 5 points?

or

What are some concepts/tools/videos I can use to learn how to construct the formulas to calculate these 4 or 5 points?

Answer 1

This is not an answer, but I wanted to paste the figure with 7 points you might need to calculate

Answer 2

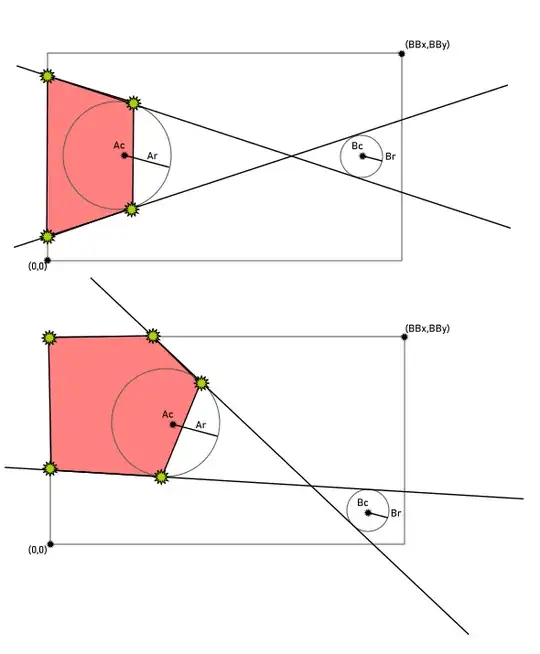
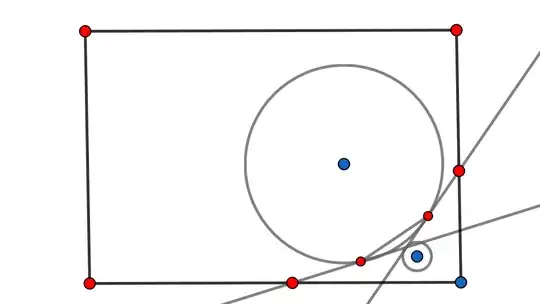
I'm going to replace the variable names $A_c, A_r, B_c, B_r$ with $C_1, r_1, C_2, r_2$ respectively.

There are several ways to tackle finding the the internal tangents between two disjoint circles. The following method uses vector and trigonometric expressions.

Consider a point $P(t)$ on the second circle, it is given by

$ P(t) = C_2 + r_2 (\cos t , \sin t ) $

The vector $(\cos t, \sin t)$ is a vector that is perpendicular to the tangent line to the circle at $P(t)$. It is pointing outward of the circle. The equation of the tangent line at $P(t)$ is,

$ (\cos t, \sin t ) \cdot ( (x, y) - P(t) ) = 0 $

We want the (signed) distance between the center of the first circle and this tangent line to be $r_1$. Hence,

$r_1 = (\cos t , \sin t ) \cdot ( C_1 - P(t) ) $

Substitute $P(t)$, you get

$ r_1 = (\cos t, \sin t ) \cdot (C_1 - C_2 - r_2 (\cos t, \sin t) )$

This simplifies to

$ r_1 = (\cos t, \sin t ) \cdot ( C_1 - C_2 ) - r_2 $

Therefore, we want to solve

$ (\cos t , \sin t ) \cdot (C_1 - C_2) = r_1 + r_2 $

If $ V = (V_x, V_y) = C_1 - C_2 $

Then

$V_x \cos t + V_y \sin t = r_1 + r_2 $

There are two solutions to this trigonometric equation, and they are given by

$ t = ATAN2( V_x, V_y ) \pm \cos^{-1} \left( \dfrac{ r_1 + r_2 }{ \sqrt{V_x^2 + V_y^2} } \right) $

The $ATAN2$ function is a standard math library function, and returns the angle $t$, which is the angle between the positive $x$ axis and the line segment extending from $(0,0)$ to $(V_x, V_y)$.

We now have two values of $t$ obtained from the above formula, so we have the equations of the two tangents.

Next, starting from $P(t)$ (where $t$ is one of the two values obtained above), we want to determine which way to move along the tangent line to meet the first circle. To do that, rotate the normal vector which is $(\cos t, \sin t)$ by $90^\circ$ counter clockwise to obtain $d(t) = (-\sin t , \cos t )$. To determine where this is the right direction to move (along the tangent line from the the second circle (B) to the first circle (A) ), calculate

$ d(t) \cdot (C_1 - C_2 ) $

if this is positive, then $d(t)$ is the right direction, otherwise we have to reverse its direction.

Now you can intersect the tangent line

$Q(s) = P(t) + s d(t) , \ s \ge 0 $

with the borders of the bounding rectangle. There are four sides whose cartesian equations are known. Substitute $Q(s)$ into the equation of each border , and solve for $s$. If $s$ is negative then discard that intersection.

In addition, you need the touching points between the tangent lines and the first circle (circle A). This distance $s$ along the direction $d(t)$ is given by

$ s = (C_1 - C_2) \cdot d(t) $

(Projection of the vector $(C_1 - C_2)$ along the unit vector $d(t)$).

Finally you want to add the corner points. To choose which corner point to include in the set of vertices of the polygon, let $E$ be a corner point, then compute the following

$ (E - P(t) ) \cdot (\cos t , \sin t ) $

If $E$ is to be included, then this quantity must be positive for both values of $t$.