40

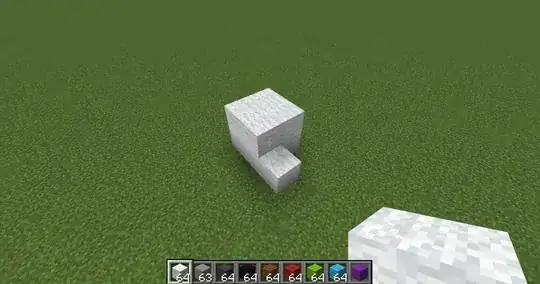
A couple of friends of mine were discussing a problem concerning this shape:

enter image description here

Is it possible to assemble enough of these to form a cube?

I have discovered a lot of impossible positions but was not successful in creating something useful. We have managed to build a 12x12x4 tower with leftover blocks at the top, however.

Maybe someone here has any ideas on how to tackle this problem? My next steps would be to try and extend our 12x12x4 tower, and if that doesn't work, to write a program to search for solutions.

RavenclawPrefect
  • 18,328
Mr Yve
  • 517
  • 14
    We can't see whether the rear bottom corner is a hole or a cubie. – shoover Oct 22 '23 at 18:11
  • 5
    This should have been a great question in Puzzling SE – Shadow Oct 23 '23 at 02:59
  • 3
    If you manage creating a block of size $a \cdot b \cdot c$, you can always turn this into a cube with size $(a \cdot b \cdot c) \cdot (a \cdot b \cdot c) \cdot (a \cdot b \cdot c)$. – Dominique Oct 23 '23 at 13:47
  • Side note: $8$ copies of the version with a hole at the back, as commented by @shoover, can be assembled into a $4 \times 4 \times 4$ cube. – nickgard Oct 26 '23 at 08:03

1 Answers1

85

Assemble four copies of the shape as shown. Four copies of the assembly create a 6x6x4 cuboid, which can be used to create a 12x12x12 cube.

enter image description here

Daniel Mathias
  • 6,133
  • In the $12\times12\times12$ cube, you are using $\frac{12^3}{9}=192$ copies of the original shape. Is it possible to show you cannot do a $6\times6\times6$ cube with $24$ original shapes? ($3\times3\times3$ with $3$ is clearly impossible and $9\times9\times9$ with $81$ seems unlikely.) – Henry Oct 23 '23 at 07:59
  • 2
    @Henry A brute force search finds no solution for $6\times6\times6$. Search on $9\times9\times9$ is currently running on my home PC while I'm at work. – Daniel Mathias Oct 23 '23 at 14:33
  • 1
    what software do you use to search for solutions? – Burnsba Oct 23 '23 at 17:37
  • 1
    @Burnsba Just some code I wrote. – Daniel Mathias Oct 23 '23 at 18:50
  • 2
    Search finished as expected: no solutions for $9\times9\times9$. There is no way to cover a $9\times9$ face while staying within the bounds of the cube. – Daniel Mathias Oct 23 '23 at 22:20
  • 3
    @Burnsba I note that this is a classic example of an exact cover problem and there are many programs already written for such problems, a famous one being Donald E. Knuth's dlx1.w; a CWEB implementation of his Algorithm X. The computational theory of polycube packings is covered in §7.2.2.1 in Volume 4B of The Art of Computer Programming; see in particular exercise 7.2.2.1–266. – ho boon suan Oct 25 '23 at 23:14