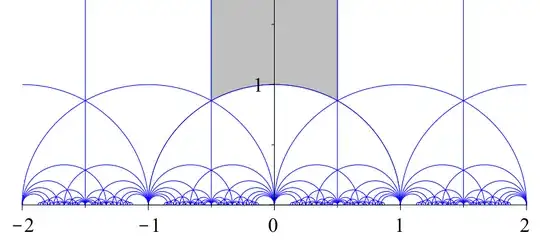
In the wiki for the Modular Group the group ($\Gamma$) is described as a $(2,3,\infty)$.
The page has a diagram for "a typical fundamental domain for the action of $\Gamma$ on the upper half-plane". I don't see how the fundamental region applies for $\Gamma$ itself...maybe for a subgroup might make more sense.
So which of these two diagrams is more accurate for the action of $\Gamma$?
The first one does look like the (regular) Dedekind tessellation, but the second makes more sense in terms of the action : I see rotations of order $2,3,\infty$ in second but only $3,\infty$ in the first.