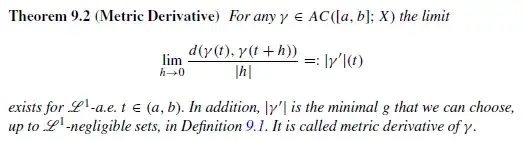Let $\mathcal{P}_2$ the space of absolutely continuous probability measures on $\mathbb{R}^d$ with finite second moment equipped with the $2$-Wasserstein metric. Fix $\mu_0, \mu_1 \in \mathcal{P}_2.$ Let $T$ be the optimal transport map from $\mu_0$ to $\mu_1.$ It is well known that the geodesic curve $\mu_t = ((1 - t) \text{id} + t T)_\# \mu_0$ is absolutely continuous.
I am wondering if the linear interpolation $\tilde \mu_t = (1 - t) \mu_0 + t \mu_1$ is absolutely continuous.
Any reference would be helpful too.
Thank you!