I have been unable to find anywhere a sharp bounding for the partial sum of the first $n$ square-free integers $\sum_{k=1}^{n} k$, where $k$ runs over the square-free integers. I guess it should be around $\frac{\pi^2}{6} \left(\frac{n^2+n}{2}\right)$, but I found no reference to check and I do not have a rigorous way to prove my guess, just the heuristic following from the partial sum of the first positive integers and the distribution of square-free numbers.
Any reference or proof of a sharp bound would be welcomed.
Thanks!
EDIT
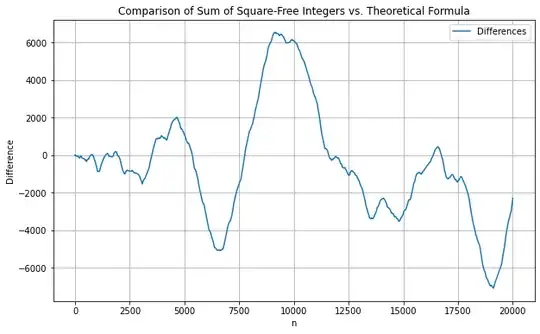
After some trial an error experimentation, it seems that $$\sum_{k=1}^{n} k = \frac{\pi^2}{6}\left(\frac{n^2+n}{2}\right)-\frac{6}{\pi^2}n\frac{\log(n)}{\log\log(n)}+O\left(\frac{n}{\sqrt{\log\log(n)}}\right)$$ Here the graphical representation of the diferences between $\sum_{k=1}^{n} k$ and $\frac{\pi^2}{6}\left(\frac{n^2+n}{2}\right)-\frac{6}{\pi^2}n\frac{\log(n)}{\log\log(n)}$:
There is still a clear pattern in the differences function, so I believe that the theoretical formula can be improved even further.
Is there any theoretical explanation supporting this formula? It seems much better than the one obtained using abelian partial summation.