$\newcommand{\cis}{\operatorname{cis}}$
To reduce fraction-clutter, I'll define $\pi_n := \pi/n$; also, I'll abuse notation to define $\cis\theta:=(\cos\theta,\sin\theta)$.
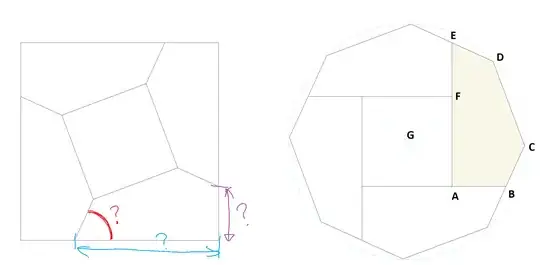
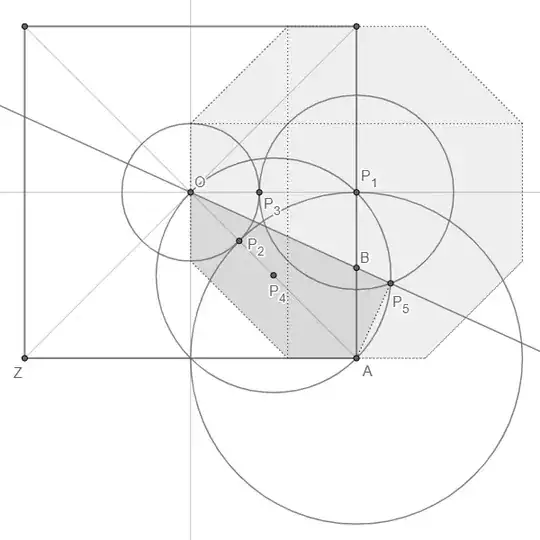
Importantly, in the octagon figure, the central square is rotated everso-slightly —just-under $2^\circ$— from being "axis-aligned". This complicates things a bit. (Or not: Skip to the Note for an uncomplicated discussion.)

Suppose the octagon has circumradius $r$, so that its sides have length $s:=2r\sin\pi_8= \sqrt{2-\sqrt{2}}$. Define points $P_k := r\,\cis k\pi_8$, for $k=0, 1, 2, \ldots, 7$; assigning OP's labels, we have $C:=P_0$ and $D:=P_1$; also, rotational symmetry in the square arrangement guarantees $|DE|=|BC|$, so that $B$ and $E$ are necessarily midpoints of segments $P_7P_0$ and $P_1P_2$, respectively.
The square arrangement also indicates that $|AF|=|CD|$, so that $|OF|=s/\sqrt{2}$. We can thus write
$$F = \frac{s}{\sqrt2}\cis\theta \qquad A = \frac{s}{\sqrt2}\cis(\theta-\pi_2)$$ for some $\theta$ that makes $A$, $E$, $F$ collinear. With a calculational assist from Mathematica, I find that $\theta\approx46.9698^\circ$ satisfies:
$$\cos\theta = \frac12 \left(\sqrt2-1\right) \left(\sqrt{2 (4 + 3 \sqrt2)} - \sqrt{2-\sqrt2}\right)$$
(Refining this value is left as an exercise to the reader.) OP's "red angle" is given by
$$\angle DEF = \frac12\cdot 135^\circ - (\theta-45^\circ) \approx 65.5302^\circ$$
Finally, we can write
$$\frac{|AF|}{|AE|} = \frac{8 \sin\pi_8}{2 + \sqrt2 + 4\sqrt2 \sin\pi_8 \cos\theta} \approx 0.62588$$
Since all the expressions here involve sums, differences, products, and ratios of nested square roots, the dissection is straightedge-and-compass constructible. See Notes for constructions.
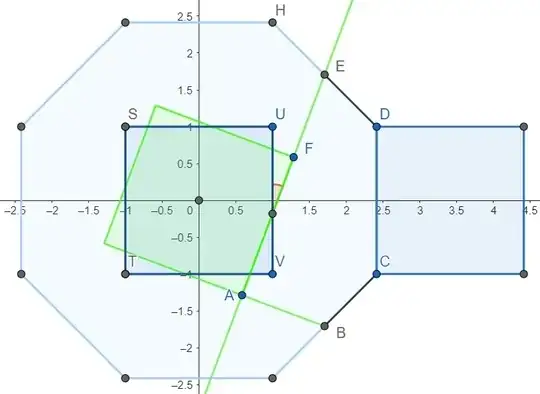
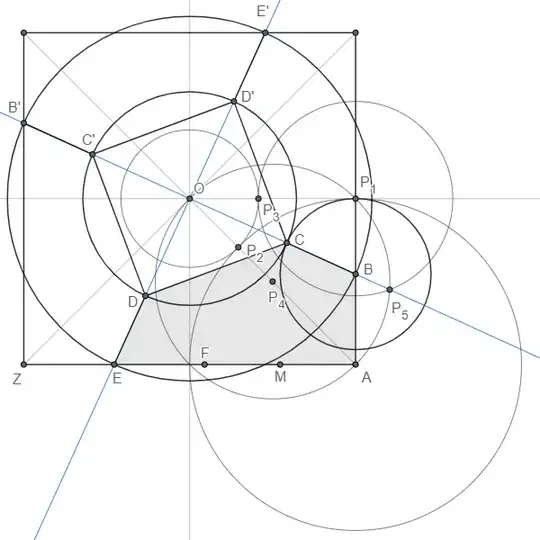
Note. Daniel Mathias helpfully demonstrates that, starting from the octagon itself, the construction of pentagon $ABCDE$ is dead-simple:
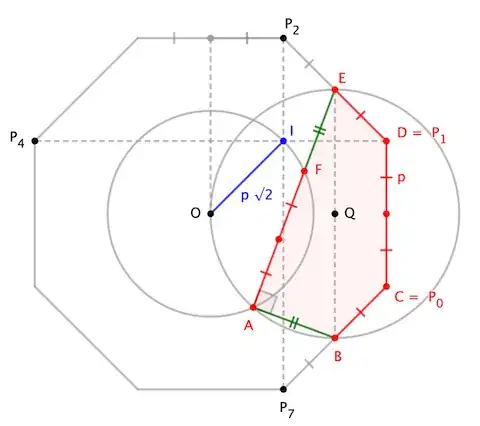
Let diagonals $P_1P_4$ and $P_2P_7$ meet at $I$, and let $\bigcirc O$ pass through $I$. Let the midpoint of $B$ and $E$ be $Q$, and let $\bigcirc Q$ pass through those points (and $O$). Then $A$ is the "lower" point where these circles meet (thanks to Thales' Theorem), and $F$ is the "other" point where line $AE$ meets $\bigcirc O$. (Verification is straightforward.)
Given that, we don't even need to know any lengths or angle-measures. Nevertheless, I'll give an easier derivation of the final ratio from my previous pass at this problem.
Let the sides of the octagon have lengths $2p$. Then we have $|AF|=|BC|=2p$ and $|BE|=2p+p\sqrt{2}=|AF|(1+\sqrt{2}/2)$. Recalling that $|EF|=|AB|$, we can invoke Pythagoras on $\triangle ABE$ thusly:
$$
\begin{align}
|AE|^2+(|AE|-|AF|)^2 = |BE|^2 &\quad\to\quad
|AE| = |AF|\cdot\frac12 \left(1 + \sqrt{2 (1 + \sqrt2)}\right) \\[4pt]
&\quad\to\quad \frac{|AF|}{|AE|}\approx 0.6255
\end{align}$$
Note 2. For a carpentry-friendly construction that starts with the square ...
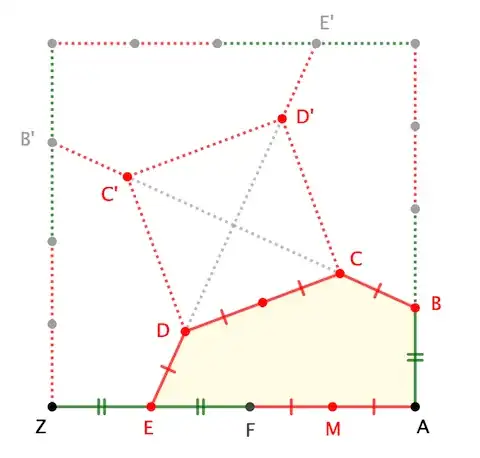
- Locate $E$ along the side $ZA$ (and corresponding points $B$, $E'$, $B'$ along the other sides), such that (leveraging previous calculations)
$$\frac{|ZE|}{|ZA|}=\frac{|AE|-|AF|}{|AE|+(|AE|-|AF|)}\approx 0.2725$$ Double-check your measurements by verifying that lines $BB'$ and $EE'$ pass through the center of the square.
- Reflect $Z$ in $E$ to get $F$
- Locate $M$ as the midpoint of segment $FA$. Define $p := |MA|$.
- Locate $C$ and $D$ along at distance $p$ from $B$ and $E$ along segments $BB'$ and $EE'$; likewise $C'$ and $D'$.
Done!
Note 3. Here's a straightedge-and-compass construction of the point $B$ in the above figure.
Let $O$ be square's center, $M$ the midpoint of its right side, and $P$ its upper-right vertex.
For follow-along calculations, take $|MP|=1$ to be half the square's side-length. Fiddling with the radical ratios above, we find that we want to construct $B$ such that $$|MB|=\frac{1}{\sqrt{2(1+\sqrt{2})}}$$ (This comports with @DanielMathias' comment to the question.)
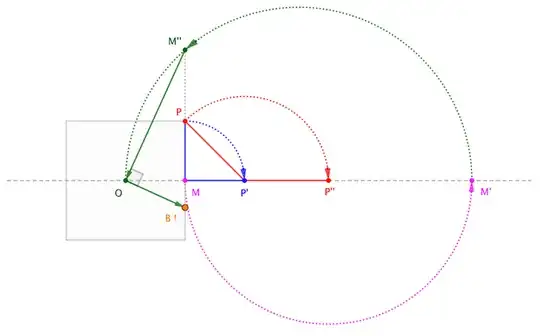
Transfer $P$ to $P'$ on the horizontal midline via rotation about $M$. $$|MP'| = 1$$
Transfer $P$ to $P''$ on the midline via rotation about $P'$. $$|MP''| = 1+\sqrt{2}$$
Transfer $M$ to $M'$ on the midline via rotation about $P''$. $$|MM'| = 2(1+\sqrt{2})$$
Transfer $M'$ to $M''$ on the side-line $MP$ via the semicircle with diameter $OM'$.
$$|MM''| = \sqrt{|MM'|} = \sqrt{2(1+\sqrt{2})}$$
Draw line $M''O$; along the perpendicular to this line at $O$, transfer $O$ to $B$ on the side-line.
$$|MB| = \frac{1}{|MM''|} = \frac{1}{\sqrt{2(1+\sqrt{2})}}$$
Done!