I noticed that any generic orthogonal projection of a cube has exactly two crossings.
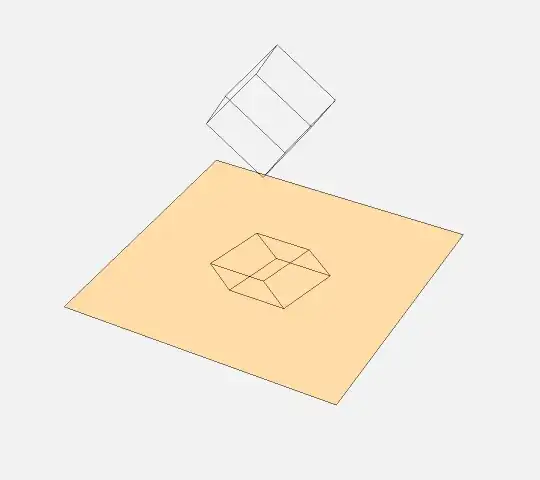This led me to wonder about generalizations. A friend suggested I look at zonohedra.
A zonohedron is the Minkowski sum of several line segments, called generators. This includes the cube, even-sided prisms, the truncated octahedron, and more. After playing around with some examples, we came across the following conjecture:
Conjecture: Any (generic) orthogonal projection of a zonohedron with $n$ generators has $2(n-2)$ crossings.
(By "generic" I mean to exclude the measure-zero set of projections for which two line segments coincide, resulting in a continuum of intersections.)
Is this conjecture true? I have no idea how to prove it; visualizing rotating complicated three-dimensional objects makes my head hurt. It's entirely possible that we just missed a counterexample.
We may also conjecture the converse:
Conjecture: If all generic orthogonal projections of a polyhedron have the same number of crossings, it is a zonohedron.
(Note that, combined with our first conjecture, this means that in this case the number of crossings must be even.)
