I wanted to study the following problem:
Let
$$x!_{(a)}=a^{\frac{x}{a}}\Gamma\left(1+\frac{x}{a}\right)\prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}$$
where
$$C_{a}(x)=\frac{1}{a}\left(1+2\sum_{k=1}^{\left\lfloor\frac{a-1}{2}\right\rfloor}\cos\left(\frac{2k\pi}{a}x\right)+\operatorname{mod}\left(a-1,2\right)\cos\left(\pi x\right)\right)$$
The analitic continuation of the multifactorial.
An alternative representation of $C_a(x)$ is: $$C_a(x)=\frac{1}{a}\sum_{k=1}^{a}\cos\left(\theta_k x\right)\qquad \text{where }\theta_k=\arccos\left(\cos\left(\frac{2k\pi}{a}\right)\right)\neq \frac{2k\pi}{a}\text{ for }k\in[1,...,a]$$
And let
$$x?_{(a)}=a^{\frac{x}{a}}\Gamma\left(1+\frac{x}{a}\right)\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_{a}(x-j)$$
The Fourier expansion of $x!_{(a)}$
I want to calculate the maximum relative error of $x?_{(a)}$ compared to $x!_{(a)}$
$\text{rel.err.}(x)=\left|\dfrac{x?_{(a)}-x!_{(a)}}{x!_{(a)}}\right|$
To calculate the maximum therefore I have to take the derivative and set it equal to $0$ (to simplify the calculations I remove the absolute value)
$\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{x?_{(a)}-x!_{(a)}}{x!_{(a)}}=\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{x?_{(a)}}{x!_{(a)}}$
$\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{x?_{(a)}-x!_{(a)}}{x!_{(a)}}=\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\displaystyle a^{\frac{x}{a}}\Gamma\left(1+\frac{x}{a}\right)\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_a\left(x-j\right)}{\displaystyle a^{\frac{x}{a}}\Gamma\left(1+\frac{x}{a}\right)\prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}}$
$\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{x?_{(a)}-x!_{(a)}}{x!_{(a)}}=\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\displaystyle \sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_a\left(x-j\right)}{\displaystyle \prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}}$
$$\color{blue}{\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\displaystyle \sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_a\left(x-j\right)}{\displaystyle \prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}}=0}$$
$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{f(x)}{g(x)}=0\;\Leftrightarrow\; f'(x)g(x)=f(x)g'(x)$$ $$\frac{\mathrm{d}}{\mathrm{d}x}\prod_{i=1}^{n}a_i^{f_i(x)}=\left(\prod_{i=1}^{n}a_i^{f_i(x)}\right)\left(\sum_{i=1}^{n}\ln(a_i)f_i'(x)\right)$$ ${\displaystyle\left[\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_{a}'\left(x-j\right)\right]\cdot\left[ \prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}\right]=\left[\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_{a}'\left(x-j\right)\right]\cdot \left[ \prod_{j=1}^{a-1}\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right)^{C_{a}\left(x-j\right)}\right]\cdot \left[ \sum_{j=1}^{a-1}\ln\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right) C'_{a}\left(x-j\right)\right]}$
$$\color{blue}{{\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_{a}'\left(x-j\right)=\left[\sum_{j=1}^{a}\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}C_{a}\left(x-j\right)\right]\cdot \left[ \sum_{j=1}^{a-1}\ln\left(\frac{a^{\frac{a-j}{a}}}{\Gamma\left(\frac{j}{a}\right)}\right) C'_{a}\left(x-j\right)\right]}}$$
This equation is a goniometric equation, in fact it depends only on $C_a(x)$ (which is the sum of goniometric functions) and its derivative. But I got stuck at this step.
I think this problem is very interesting for 3 reasons:
- The Fourier expansion of the multifactorial is a finite sum and not a series, therefore the maximum of the relative error it is a fixed value, once $a$ is chosen.
- The equation to find the maximum relative error is a goniometric equation, therefore it follows a periodic trend and remains limited as $x$ increases.
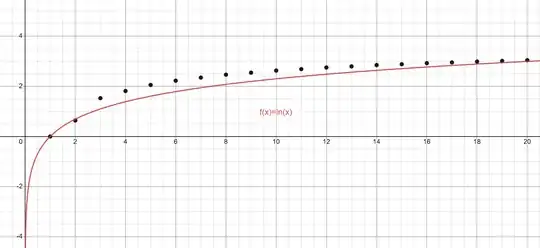
- By representing the trend of the maximum relative error, we see that in addition to being very small, it has a less than logarithmic trend.
So I would like to see what happens as $a$ increases (if it grows unlimitedly or converges to some value)
Here is a table of the values I found:
$$\begin{array}{|c|c|}\hline a&\text{max. rel. err.}\\\hline 1&=0.000\%\\ 2&\approx 0.639\%\\ 3&\approx 1.530\%\\ 4&\approx 1.814\%\\ 5&\approx 2.056\%\\ 6&\approx 2.225\%\\ 7&\approx 2.350\%\\ 8&\approx 2.465\%\\ 9&\approx 2.546\%\\ 10&\approx 2.630\%\\ 11&\approx 2.688\%\\ 12&\approx 2.752\%\\ 13&\approx 2.796\%\\ 14&\approx 2.848\%\\ 15&\approx 2.883\%\\ 16&\approx 2.925\%\\ 17&\approx 2.954\%\\ 18&\approx 2.989\%\\ 19&\approx 3.013\%\\ 20&\approx 3.043\%\\ ...&...\\ 100&\approx 3.562\%\\ 200&\approx 3.663\%\\ 500&\approx 3.736\%\\ 1000&\approx 3.766\%\\\hline \end{array}$$
Edit
I think it's useful that: $$\lim_{a\to\infty}C_a(x)=\frac{\sin(\pi x)}{\pi x}$$